Как найти диагональ параллелепипеда по объему — формула и примеры расчета — находим длину относительно трех граней

Параллелепипед - это геометрическое тело, у которого все грани являются прямоугольниками, а все углы - прямыми. Одним из основных параметров параллелепипеда является его объем, который показывает, сколько пространства занимает данная фигура. Но что делать, если известен только объем параллелепипеда, а требуется найти его диагональ? В этой статье мы рассмотрим формулу для расчета диагонали параллелепипеда по объему, а также приведем несколько примеров расчета.

Итак, чтобы найти диагональ параллелепипеда по его объему, нам понадобится знание формулы для вычисления объема данной фигуры. Объем параллелепипеда равен произведению его трех измерений: длины, ширины и высоты. Формула для расчета объема параллелепипеда выглядит следующим образом: V = a * b * h, где V - объем, a - длина, b - ширина, h - высота параллелепипеда.

Для нахождения диагонали параллелепипеда по объему можно воспользоваться следующими шагами:

1. Найдите объем параллелепипеда с помощью известной формулы V = a * b * h, где a, b и h - известные величины.
2. Выразите диагональ параллелепипеда через объем и другие параметры. Формула для вычисления диагонали: d = 3√(4V/√(a^2b^2+a^2h^2+b^2h^2)), где V - объем параллелепипеда, a - длина, b - ширина, h - высота параллелепипеда.
3. Подставьте значения известных параметров в формулу для диагонали и выполните необходимые вычисления.

Рассмотрим пример. Пусть у нас есть параллелепипед со следующими размерами: длина - 6 см, ширина - 4 см, высота - 3 см. Найдем его объем: V = 6 * 4 * 3 = 72 см³. Теперь, подставив значения в формулу для диагонали, получаем: d = 3√(4 * 72 / √(6^2 * 4^2 + 6^2 * 3^2 + 4^2 * 3^2)) ≈ 8.25 см. Таким образом, диагональ данного параллелепипеда составляет около 8.25 см.

Как найти диагональ параллелепипеда

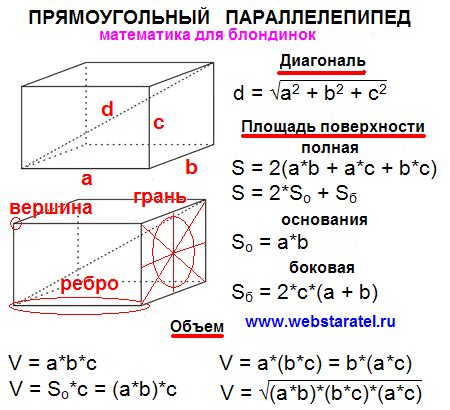
Для того чтобы найти диагональ параллелепипеда, вам понадобится знать длину, ширину и высоту фигуры. Для удобства будем обозначать их соответственно a, b и c.

Формула для нахождения длины диагонали параллелепипеда определяется по теореме Пифагора:

d = √(a² + b² + c²),

где d - искомая диагональ параллелепипеда.

Пример:

Пусть у нас есть параллелепипед со сторонами a = 3, b = 4 и c = 5. Используя формулу, мы можем найти его диагональ:

d = √(3² + 4² + 5²) = √(9 + 16 + 25) = √50 ≈ 7.07.

Таким образом, длина диагонали этого параллелепипеда около 7.07.

Найденная диагональ может быть полезной, например, при выборе упаковки или расчете пролета в строительстве. Имейте в виду, что если вам изначально известен объем параллелепипеда, можно воспользоваться другой формулой для нахождения длины его диагонали.

Определение и основная формула

Для расчета длины диагонали параллелепипеда по известному объему можно воспользоваться следующей формулой:

d = ∛(6V)

Где:

• d – длина диагонали параллелепипеда.
• V – объем параллелепипеда.

Найденная длина диагонали помогает определить, насколько вытянутым или сплющенным является параллелепипед.

Примеры расчета диагонали параллелепипеда

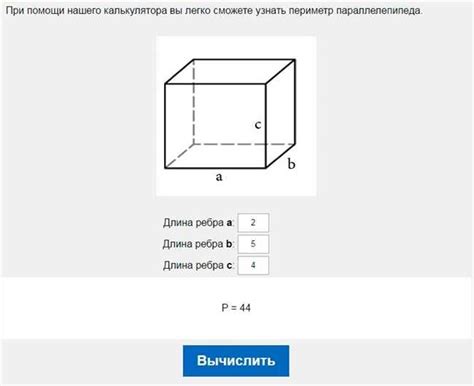
Для определения диагонали параллелепипеда по известному объему необходимо знать значения длины, ширины и высоты параллелепипеда. С использованием указанных параметров, можно применить следующую формулу:

Диагональ = √(a² + b² + c²)

Где:

• a - длина параллелепипеда
• b - ширина параллелепипеда
• c - высота параллелепипеда

Приведем пример расчета диагонали параллелепипеда:

Пусть у нас есть параллелепипед с длиной a = 5, шириной b = 3 и высотой c = 4. Найдем диагональ:

Диагональ = √(5² + 3² + 4²) = √(25 + 9 + 16) = √50 = 7.07

Таким образом, диагональ данного параллелепипеда равна 7.07 единиц.

Используя данную формулу и знание значений длины, ширины и высоты параллелепипеда, можно легко определить его диагональ.

Для расчета диагонали параллелепипеда по объему, необходимо знать только значение объема и формулу для вычисления диагонали. Формула для вычисления диагонали параллелепипеда по объему имеет вид:

Диагональ = ∛(6 * объем / (√(3)))

Чтобы применить эту формулу, достаточно знать объем параллелепипеда, который можно измерить или получить из исходных данных. Далее, подставив значение объема в формулу, можно вычислить диагональ параллелепипеда.

Найденное значение диагонали будет являться ответом на задачу по расчету диагонали параллелепипеда по объему.