Как найти диагональ правильного шестиугольника без применения формул и математики

Шестиугольник – это многоугольник с шестью сторонами и шестью углами. Все его стороны имеют одинаковую длину, а все углы равны 120 градусам. Правильный шестиугольник обладает рядом особых свойств и характеристик, одна из которых – его диагональ. Диагональ – это отрезок, соединяющий два несмежных вершины многоугольника. В данной статье мы рассмотрим, как найти диагональ правильного шестиугольника.

Для нахождения диагонали правильного шестиугольника необходимо знать его сторону. Для этого можно использовать различные способы. Например, если шестиугольник вписан в окружность, то его сторона будет равна длине радиуса окружности. Другой способ – известна длина одной из сторон шестиугольника, а остальные стороны можно выразить через нее с помощью геометрических формул.

Зная длину стороны правильного шестиугольника, можно найти его диагональ с помощью некоторых математических формул. Длина диагонали шестиугольника зависит от его стороны и составляет два радиуса описанной окружности. Формулу для вычисления диагонали шестиугольника можно записать следующим образом:

Диагональ = 2 * Радиус

Таким образом, зная длину стороны правильного шестиугольника, вы можете легко и быстро вычислить его диагональ с помощью данной формулы. Эта информация может быть полезна в различных областях, таких как геометрия, архитектура, дизайн и другие.

Определение правильного шестиугольника

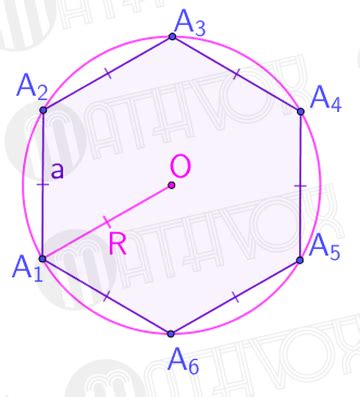
Для того чтобы определить, является ли шестиугольник правильным, можно использовать несколько критериев:

1. У всех сторон должна быть одинаковая длина. Для этого можно измерить длину каждой стороны и сравнить их значения. Если все стороны одинаковы, то шестиугольник правильный.

2. У всех углов должна быть одинаковая мера. Для этого можно измерить угол каждого вершины с помощью транспортира и сравнить значения. Если все углы равны 120 градусов, то шестиугольник правильный.

3. Можно провести диагонали шестиугольника. Если диагонали пересекаются в одной точке и делят шестиугольник на шесть равных треугольников, то шестиугольник правильный.

Правильный шестиугольник является одним из семи правильных многоугольников, и он имеет свои уникальные свойства и характеристики. Исследование и изучение правильных многоугольников важны в геометрии и математике в целом.

Что такое правильный шестиугольник?

Углы в правильном шестиугольнике равны 120 градусам, что делает его особенно интересным и привлекательным для исследования. Он также имеет шесть равных сторон, что делает его устойчивым и прочным, а также идеальным для решения различных задач и заданий в математике.

Правильные шестиугольники имеют множество применений и областей применения. Они могут использоваться в строительстве, дизайне, архитектуре и других сферах, где требуется высокая степень точности и симметрии. Они также играют важную роль в математике и геометрии, где являются объектом исследования различных теоретических моделей и алгоритмов.

Важно отметить, что правильный шестиугольник является особым и уникальным видом фигуры, который обладает своими особенностями и свойствами. Изучение и понимание этих особенностей позволяет лучше понять мир геометрии и применить полученные знания в практических задачах.

Значение диагонали в правильном шестиугольнике

Чтобы найти значение диагонали в правильном шестиугольнике, необходимо использовать формулу.

Формула для нахождения длины диагонали шестиугольника: Диагональ = 2 * сторона * sin(30°)

Здесь, сторона шестиугольника - это длина одной из его сторон, а sin(30°) - синус 30 градусов.

Применение этой формулы позволяет найти значение диагонали в правильном шестиугольнике с помощью известных данных о его сторонах.

Например, если длина стороны шестиугольника равна 5 сантиметров, то диагональ будет равна:

Таким образом, диагональ в правильном шестиугольнике со стороной длиной 5 сантиметров будет примерно равна 5 сантиметрам.

Зная формулу для нахождения диагонали в правильном шестиугольнике, можно вычислить ее значение для любого размера стороны и использовать это знание при решении различных геометрических задач.

Какая роль играет диагональ в правильном шестиугольнике?

Одна из главных особенностей диагоналей в правильном шестиугольнике заключается в том, что все они равны друг другу. Это значит, что любая диагональ в таком шестиугольнике будет иметь одну и ту же длину. Такая равность диагоналей обусловлена симметрией и регулярностью фигуры.

Диагонали в правильном шестиугольнике также играют важную роль при вычислении его площади и периметра. Площадь шестиугольника можно найти, используя формулу: площадь = (3√3/2) * длина стороны в квадрате. Диагонали помогают разделить фигуру на равные треугольники, которые затем могут быть анализированы и использованы для расчета площади.

Кроме того, диагонали влияют на углы шестиугольника. Например, угол между диагональю и стороной будет половиной угла между диагоналями, так как они делятся в точке пересечения. Это свойство позволяет использовать диагонали для нахождения углов внутри шестиугольника.

Таким образом, диагонали играют важную роль в свойствах, структуре и вычислениях, касающихся правильного шестиугольника. Они обеспечивают равность сторон, помогают определить площадь и периметр фигуры, а также влияют на углы внутри шестиугольника.

Как вычислить длину диагонали в правильном шестиугольнике

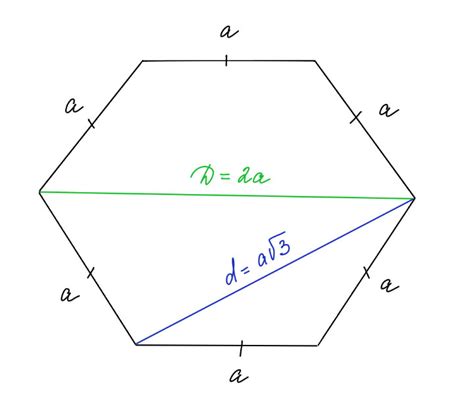
Для вычисления длины диагонали в правильном шестиугольнике можно использовать геометрические свойства фигуры.

Шестиугольник является правильным, если все его стороны равны, а углы между сторонами равны 120 градусам.

Для вычисления длины диагонали в правильном шестиугольнике можно использовать формулу:

d = s * √3, где d - длина диагонали, s - длина стороны шестиугольника.

Для примера, если длина стороны шестиугольника равна 10 см, то длина диагонали будет равна:

d = 10 * √3 ≈ 17.32 см.

Таким образом, чтобы вычислить длину диагонали в правильном шестиугольнике, необходимо знать длину стороны и применить формулу.

Определение длины диагонали

Для нахождения длины диагонали правильного шестиугольника необходимо выполнить следующие шаги:

1. Определите длину стороны шестиугольника. Это может быть дано в условии задачи или требовать отдельных расчетов на основе других параметров.
2. Вычислите длину одной стороны треугольника, образующего шестиугольник. Для этого необходимо разделить длину стороны шестиугольника на 6.
3. Используя длину одной стороны треугольника, найдите значение его высоты. Для правильных шестиугольников, высота равна длине стороны, умноженной на √3.
4. По теореме Пифагора вычислите длину диагонали треугольника, используя найденные ранее значения длины стороны и высоты. Диагональ равна √(сторона^2 + (0,5*высота)^2).
5. Умножьте полученную длину диагонали треугольника на 2, чтобы найти длину диагонали правильного шестиугольника, так как в нем две диагонали.

Таким образом, длину диагонали правильного шестиугольника можно определить, зная длину стороны.

Формула для нахождения длины диагонали правильного шестиугольника

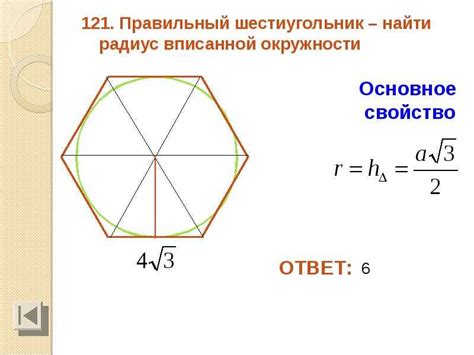
Для нахождения длины диагонали правильного шестиугольника можно использовать следующую формулу:

Диагональ = сторона × √3

Где:

• Диагональ - длина диагонали;
• Сторона - длина стороны шестиугольника;
• √3 - квадратный корень из числа 3, примерное значение 1.732.

Эта формула основана на свойстве правильного шестиугольника, согласно которому диагональ делит угол между смежными сторонами на три равные части. Поэтому, зная длину стороны шестиугольника, можно найти длину диагонали, умножив длину стороны на квадратный корень из 3.

Например, если сторона шестиугольника равна 5 единицам, то длина диагонали будет:

Диагональ = 5 × √3 ≈ 8.66 единиц.

Используя данную формулу, можно легко и быстро находить длину диагонали правильного шестиугольника при известной длине его стороны.