Диагональ прямоугольного параллелепипеда – это линия, соединяющая два противоположных вершины. Нахождение диагонали важно для различных задач, например, при расчёте объёма или определении габаритов. Для нахождения диагонали параллелепипеда существуют специальные формулы, основанные на его геометрических характеристиках. В этой статье мы расскажем о том, как найти диагональ прямоугольного параллелепипеда и приведем примеры расчетов.
Если известны все три стороны прямоугольного параллелепипеда, можно использовать теорему Пифагора для нахождения диагонали. Формула для этого случая выглядит следующим образом:
d = √(a² + b² + c²),
где d – диагональ прямоугольного параллелепипеда,
a, b, c – стороны параллелепипеда.
Для более наглядного понимания лучше рассмотреть пример. Предположим, что стороны нашего параллелепипеда равны 4, 3 и 2. Применяя формулу, мы получаем:
d = √(4² + 3² + 2²) = √(16 + 9 + 4) = √29 ≈ 5.39.
Таким образом, диагональ прямоугольного параллелепипеда с данными сторонами примерно равна 5.39.
Что такое диагональ прямоугольного параллелепипеда
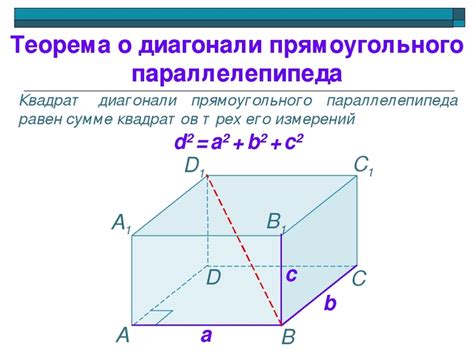
Для нахождения диагонали прямоугольного параллелепипеда можно воспользоваться теоремой Пифагора. Если известны длины трех ребер параллелепипеда (a, b и c), то длину диагонали (d) можно найти по формуле:
d = √(a² + b² + c²)
Зная размеры параллелепипеда, можно рассчитать его диагональ и использовать эту информацию, например, для определения размеров упаковки, необходимой для хранения или отправки предметов.
Рассмотрим пример: пусть у нас есть прямоугольный параллелепипед с длинами ребер a = 3 см, b = 4 см и c = 5 см. Чтобы найти диагональ (d), подставим значения в формулу:
d = √(3² + 4² + 5²) = √(9 + 16 + 25) = √(50) ≈ 7.07 см
Таким образом, длина диагонали прямоугольного параллелепипеда составляет около 7.07 см.
Знание диагонали параллелепипеда важно при проектировании и строительстве, расчете объемов и площадей, а также в других областях, где необходимо учитывать размеры этого трехмерного объекта.
Определение и значения

Диагональ прямоугольного параллелепипеда представляет собой отрезок, соединяющий две противоположные вершины этого параллелепипеда, проходящий по его внутренней части.
Значение диагонали прямоугольного параллелепипеда имеет важное значение при решении различных задач и формул, связанных с этой геометрической фигурой. Например, для нахождения объема параллелепипеда, длину его ребер или площади его боковой поверхности требуется знание длины диагонали.
Зная значения длин ребер прямоугольного параллелепипеда, можно вычислить длину диагонали с помощью формулы:
- Для прямоугольного параллелепипеда с ребрами a, b и c длина диагонали (d) определяется по формуле: d = √(a² + b² + c²).
- Для куба (специального вида прямоугольного параллелепипеда, у которого все ребра равны) со стороной a длина диагонали (d) определяется по формуле: d = √(3a²).
Таким образом, диагональ прямоугольного параллелепипеда играет важную роль при решении задач, связанных с данным геометрическим объектом, позволяя определить длину и другие параметры этой фигуры.
Как найти длину диагонали прямоугольного параллелепипеда
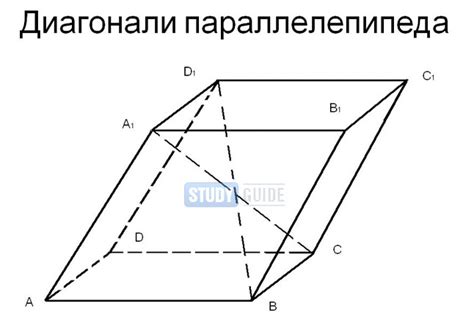
Для нахождения длины диагонали прямоугольного параллелепипеда необходимо знать значения всех трех его измерений: длину (a), ширину (b) и высоту (c).
Для прямоугольного параллелепипеда с измерениями a, b и c, длина диагонали (d) может быть найдена с помощью формулы:
| Формула |
|---|
d = √(a² + b² + c²) |
Где d - длина диагонали, a, b и c - значение каждого измерения.
Давайте рассмотрим пример:
Представим прямоугольный параллелепипед со следующими измерениями:
| Длина (a) | Ширина (b) | Высота (c) |
|---|---|---|
| 6 | 8 | 10 |
Используя формулу, мы можем вычислить длину диагонали:
d = √(6² + 8² + 10²) = √(36 + 64 + 100) = √200 ≈ 14.14
Таким образом, длина диагонали прямоугольного параллелепипеда с измерениями 6, 8 и 10 равняется примерно 14.14 единицы длины.
Формула диагонали

Для вычисления диагонали прямоугольного параллелепипеда вам понадобится знать длину, ширину и высоту этой фигуры. Диагональ можно получить, применяя теорему Пифагора на трехмерный мир.
Таким образом, формула для вычисления диагонали прямоугольного параллелепипеда выглядит следующим образом:
Диагональ = √(длина^2 + ширина^2 + высота^2)
Где √ обозначает квадратный корень, а ^2 означает возведение в квадрат. Имейте в виду, что все размеры должны быть выражены в одной единице измерения, например, в сантиметрах или метрах.
Пример:
Пусть длина параллелепипеда равна 5 сантиметров, ширина - 3 сантиметра, и высота - 4 сантиметра. Для вычисления диагонали нужно подставить значения в формулу:
Диагональ = √(5^2 + 3^2 + 4^2) = √(25 + 9 + 16) = √50 = 7.07 сантиметра
Таким образом, диагональ прямоугольного параллелепипеда, заданного своими размерами, равна 7.07 сантиметра.
Примеры расчета

Для лучшего понимания как найти диагональ прямоугольного параллелепипеда, рассмотрим несколько примеров.
Пример 1:
Пусть у нас есть прямоугольный параллелепипед с длиной (а) равной 6 см, шириной (b) равной 4 см и высотой (с) равной 3 см. Найдем диагональ параллелепипеда (d):
d = √(a² + b² + c²)
d = √(6² + 4² + 3²)
d = √(36 + 16 + 9)
d = √61
d ≈ 7.81 см
Таким образом, диагональ этого параллелепипеда составляет примерно 7.81 см.
Пример 2:
У нас есть другой прямоугольный параллелепипед с длиной (а) равной 10 см, шириной (b) равной 8 см и высотой (с) равной 5 см. Найдем диагональ параллелепипеда (d):
d = √(a² + b² + c²)
d = √(10² + 8² + 5²)
d = √(100 + 64 + 25)
d = √189
d ≈ 13.75 см
Следовательно, диагональ этого параллелепипеда примерно равна 13.75 см.
Теперь вы знаете, как вычислить диагональ прямоугольного параллелепипеда с помощью формулы и можете применить ее в своих расчетах.
Значимость диагонали в реальной жизни

Например, при покупке новой телевизионной панели или компьютерного монитора важно знать его диагональ, чтобы понять, как она будет вписываться в имеющееся пространство или мебель. Длина диагонали также может помочь определить, насколько удобен будет просмотр изображения или чтение текста на экране.
Диагональ прямоугольного параллелепипеда также может быть полезна при создании упаковки или контейнера для товаров. Если известна длина диагонали, можно определить минимальные размеры контейнера, чтобы предметы поместились в него правильно и без повреждений.
Кроме того, знание длины диагонали может быть важным при строительстве или ремонте. Например, при укладке плитки или настиле пола, знание длины диагонали поможет правильно расположить элементы и предотвратить зависание или смещение предметов. Также, при создании рамок для картин и зеркал, знание длины диагонали позволяет правильно выбрать размер и конструкцию рамы.
В общем, понимание диагонали прямоугольного параллелепипеда может быть полезным во многих ситуациях в нашей повседневной жизни. Она помогает нам рационально использовать пространство, избегать ошибок и создавать здоровую и эффективную среду.