Ромб - это уникальная геометрическая фигура, которая характеризуется особыми свойствами. Если у вас есть ромб, то, возможно, вы захотите найти его диагональ, зная только одну из сторон и один из углов. Это особенно полезно, если у вас нет возможности измерить диагональ непосредственно.
Для расчета диагонали ромба по стороне и углу существует специальная формула, которую можно использовать. Но прежде чем мы перейдем к расчетам, нужно разобраться в некоторых основных понятиях. Диагональ ромба - это отрезок, соединяющий два противоположных угла. Он разделяет ромб на два равных треугольника. Сторона ромба - это любая сторона ромба, а угол ромба - это угол между двумя смежными сторонами.
Теперь давайте разберемся с формулой. Если у вас есть длина одной стороны ромба (a) и значение одного из его углов (α), вы можете найти длину диагонали ромба (d) с помощью следующей формулы:
d = 2 * a * sin(α/2)
Таким образом, зная длину стороны ромба и значение одного из его углов, вы можете легко расчитать длину диагонали. Теперь у вас есть все необходимые знания, чтобы найти диагональ ромба по стороне и углу с помощью простой формулы расчета.
Что такое диагональ ромба?

Главная диагональ ромба - это отрезок, который соединяет вершины, расположенные наиболее удаленно друг от друга. Она делит ромб на два равных треугольника и служит осью симметрии.
Побочная диагональ ромба - это отрезок, который соединяет вершины, расположенные наименее удаленно друг от друга. Она также делит ромб на два равных треугольника, однако побочная диагональ не является осью симметрии.
Длина диагоналей ромба может быть найдена с использованием формулы, которая зависит от известных параметров ромба, таких как длина стороны или угол.
Обратите внимание, что в ромбе диагонали всегда перпендикулярны друг другу, и каждая диагональ является биссектрисой соответствующего угла.
Диагональ ромба: определение и свойства
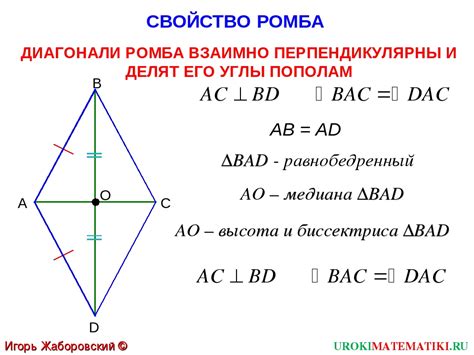
Диагональ ромба имеет ряд свойств:
| Свойство | Описание |
| Длина диагонали | Длина диагонали ромба может быть вычислена с помощью специальной формулы, используя длину одной из его сторон и величину одного из его углов. |
| Перпендикулярность | Диагонали ромба пересекаются под прямым углом. Это означает, что угол между диагоналями ромба всегда равен 90 градусам. |
| Равенство диагоналей | Все диагонали ромба равны по длине. Это свойство следует из равенства его сторон. |
Знание свойств диагонали ромба позволяет эффективно вычислять и использовать ее в различных задачах геометрии и строительства.
Как найти диагональ ромба по стороне и углу?

Если известны сторона ромба a и угол между диагоналем и этой стороной α, то для расчета диагонали ромба можно воспользоваться следующей формулой:
d = a * √(2 - 2 * cos(α))
Где d - диагональ ромба, a - сторона ромба, α - угол между диагональю и стороной.
Если известны другие параметры, например, диагональ ромба и одна из сторон, можно использовать альтернативные формулы для расчета:
- Для нахождения диагонали ромба по диагонали и стороне: d = √(a^2 + b^2)
- Для нахождения диагонали ромба по площади и стороне: d = 2 * √(S / a)
Правильно использовать формулы для расчета диагонали ромба важно, чтобы получить точный результат. Учтите, что значения стороны и угла должны быть в одинаковых единицах измерения.
Формула расчета диагонали ромба

Для расчета диагонали ромба по известной стороне и углу между этой стороной и диагональю можно воспользоваться следующей формулой:
- Получите значение стороны ромба, учитывая единицы измерения.
- Получите значение угла между известной стороной и диагональю в градусах.
- Преобразуйте значение угла в радианы, умножив его на π/180.
- Используя полученные значения, примените следующую формулу для расчета диагонали ромба:
диагональ = сторона * 2 * cos(угол)
Убедитесь, что используете функцию cos для расчета косинуса угла.
Помните, что в этой формуле размерности стороны и диагонали должны быть согласованы. Например, если сторона ромба задана в сантиметрах, то и диагональ будет получена в сантиметрах.
Используйте эту формулу для расчета диагонали ромба, чтобы быстро и точно получить необходимую информацию о вашей фигуре.
Примеры решения задачи

Рассмотрим несколько примеров решения задачи на поиск диагонали ромба по известной стороне и углу.
Пример 1: Дан ромб со стороной длиной 8 см и одним из углов 60 градусов. Найдем диагональ этого ромба.
Сначала найдем другие углы ромба. Так как все углы ромба равны, то в данном случае все углы будут равны 60 градусов.
Для нахождения диагонали можно воспользоваться теоремой синусов. Для этого возьмем половину стороны ромба, так как половина диагонали будет равной половине стороны (8/2 = 4 см).
Получаем:
sin(60°) = (4 см) / d
d = (4 см) / sin(60°)
Подсчитывая значение sin(60°) получаем:
d = (4 см) / ( √3 / 2 ) ≈ 4 см / 0.866 ≈ 4.618 см
Ответ: Диагональ ромба примерно равна 4.618 см.
Пример 2: Дан ромб со стороной длиной 12 см и одним из углов 45 градусов. Найдем диагональ этого ромба.
Так как все углы ромба равны, то в данном случае все углы будут равны 45 градусов.
Используя ту же формулу, получаем:
d = (6 см) / sin(45°)
sin(45°) = 1 / √2 ≈ 0.707
d = (6 см) / 0.707 ≈ 8.485 см
Ответ: Диагональ ромба примерно равна 8.485 см.
Таким образом, для нахождения диагонали ромба по известной стороне и углу следует использовать формулу d = s / sin(α), где d - диагональ, s - сторона, α - угол.