Трапеция - это геометрическая фигура, которая имеет два параллельных основания и две непараллельные стороны. Диагональ трапеции - это отрезок, который соединяет непараллельные стороны фигуры. Нахождение диагонали трапеции может быть полезным для решения различных геометрических задач.
Существует формула, позволяющая найти диагональ трапеции по известным основаниям и высоте фигуры. Формула имеет вид:
диагональ = √(основание1^2 + основание2^2 + 2 * высота^2)
Для нахождения диагонали трапеции необходимо знать значения обоих оснований и высоту, которая является перпендикуляром к обоим основаниям. Подставив известные значения в формулу, мы получим длину диагонали.
Рассмотрим пример: Пусть у нас есть трапеция с основаниями длинной 5 и 8 и высотой 4. Чтобы найти диагональ, мы подставим значения в формулу:
диагональ = √(5^2 + 8^2 + 2 * 4^2) = √(25 + 64 + 32) = √121 = 11
Таким образом, длина диагонали трапеции равна 11.
Определение диагонали трапеции и ее значение
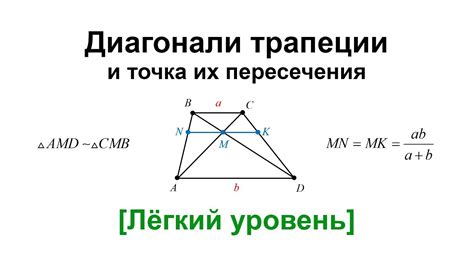
Значение диагонали трапеции можно определить с помощью формулы:
| Диагональ (d) | Основание 1 (a) | Основание 2 (b) |
| Прямоугольная трапеция: | d = sqrt((a^2) + (b^2)) | |
| Равнобедренная трапеция: | d = sqrt((2 * a^2) - (b^2)) | |
| Произвольная трапеция: | d = sqrt((a^2) + (b^2) - (2 * a * b * cos(θ))) | где θ - угол, образованный диагональю и основанием 1 |
Найдя значение диагонали трапеции, можно использовать его для решения различных задач, связанных с этой геометрической фигурой, например для вычисления площади или периметра трапеции.
Формула для вычисления диагонали трапеции

Для вычисления диагонали трапеции по известным основаниям и высоте используется следующая формула:
| Диагональ (d) | = | √((a + b)² + h²) |
Где:
- Диагональ (d) - длина диагонали трапеции
- Основания (a и b) - длины оснований трапеции
- Высота (h) - высота трапеции
С помощью данной формулы можно легко и точно определить длину диагонали трапеции, зная длины ее оснований и высоту. Например, если основания трапеции равны 8 и 12, а высота равна 5, то:
| Диагональ (d) | = | √((8 + 12)² + 5²) | = | √(20² + 5²) | = | √(400 + 25) | = | √425 | ≈ | 20.62 |
Таким образом, длина диагонали трапеции составляет примерно 20.62 единицы длины.
Пример 1: Расчет диагонали трапеции с известными основаниями
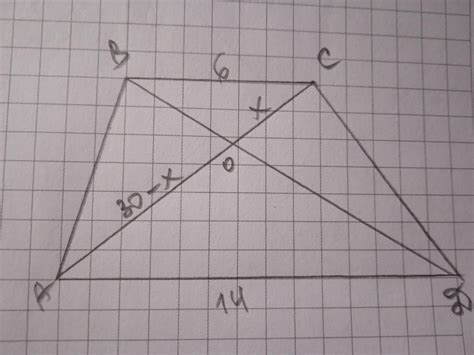
Для расчета диагонали трапеции, если известны длины ее оснований, можно использовать следующую формулу:
d = √(a2 + b2 - 2abcosα)
Где d - диагональ трапеции, a и b - длины оснований, α - угол между основаниями.
Рассмотрим конкретный пример. Пусть длина большего основания трапеции равна 8 см, а длина меньшего основания - 4 см. Известно также, что угол между основаниями равен 60 градусов.
Используя формулу, подставим значения и рассчитаем диагональ трапеции:
d = √(82 + 42 - 2 * 8 * 4 * cos60°)
d = √(64 + 16 - 64 * 4 * 0.5)
d = √(64 + 16 - 128)
d = √(80 - 128)
d = √(-48)
Поскольку значение выражения √(-48) не определено в рамках вещественных чисел, мы не можем рассчитать диагональ данной трапеции с заданными параметрами.
В данном случае трапеция не является реально существующей, так как длина диагонали не может быть определена по заданным параметрам оснований и углу.
Пример 2: Поиск диагонали трапеции с известными высотой и боковой стороной
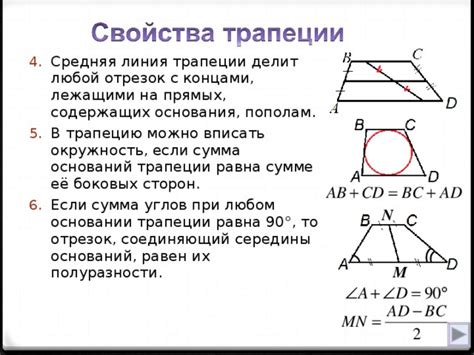
Рассмотрим трапецию ABCD, в которой известны высота и одна из боковых сторон. Необходимо найти длину диагонали.
Пусть высота трапеции равна h, а длина одной из боковых сторон равна a. Диагональ трапеции обозначим как d.
Чтобы найти диагональ, воспользуемся теоремой Пифагора для прямоугольного треугольника ADE:
d2 = a2 + h2
Возведем в квадрат обе стороны уравнения и выразим диагональ:
d = √(a2 + h2)
Таким образом, длину диагонали трапеции можно найти, зная длину одной из боковых сторон и высоту.
Например, рассмотрим трапецию ABCD, в которой высота равна 4 см, а одна из боковых сторон равна 5 см. Подставим значения в формулу:
d = √(52 + 42)
d = √(25 + 16)
d = √41
d ≈ 6.40
Таким образом, длина диагонали трапеции составляет приближенно 6.40 см.