Диагональ треугольника - это отрезок, соединяющий два его угла, не являющихся смежными. Нахождение диагонали треугольника может быть полезным для решения различных геометрических задач и вычислений. В данной статье мы рассмотрим, как найти диагональ треугольника при заданных сторонах и угле.
Существует несколько способов нахождения диагонали треугольника, в зависимости от имеющихся данных. Один из самых простых способов - использование теоремы косинусов. Для этого необходимо знать длины двух сторон треугольника и величину внутреннего угла между ними.
Формула нахождения диагонали треугольника с использованием теоремы косинусов выглядит следующим образом:
d^2 = a^2 + b^2 - 2ab * cos(C)
где d - длина диагонали треугольника, a и b - длины сторон треугольника, C - величина внутреннего угла между сторонами a и b.
Теперь, имея все необходимые данные, можно приступить к расчетам. Просто подставьте значения в формулу и выполните соответствующие математические действия, чтобы найти длину диагонали треугольника.
Что такое диагональ треугольника?

В треугольнике ABC, диагональ может быть нарисована между вершинами A и C, A и B, или B и C, в зависимости от того, какие вершины соединяются. Диагональ играет важную роль в геометрии треугольников, так как она позволяет определить длину, направление и угол между отрезками треугольника.
Длина диагонали треугольника может быть вычислена с использованием теоремы Пифагора или правила косинусов, в зависимости от доступных данных. Зная длины сторон треугольника, можно вычислить длину диагонали с помощью формулы.
Диагональ треугольника может также служить опорой для других вычислений и теорем в геометрии. Например, она может быть использована для вычисления площади треугольника с помощью формулы Герона или для доказательства некоторых свойств треугольника с помощью теоремы Косинусов.
Как узнать, какая длина диагонали у треугольника?

Если у вас есть длины всех трех сторон треугольника, вы можете использовать формулу Косинуса для вычисления длины любой диагонали. Формула Косинуса гласит: d² = a² + b² - 2ab*cos(C), где d - длина диагонали, a и b - длины сторон треугольника, C - угол между этими сторонами.
Если у вас нет длин сторон треугольника, но у вас есть координаты его вершин в плоскости, вы можете использовать формулу расстояния между двумя точками для вычисления длины диагонали. Формула расстояния между двумя точками в плоскости гласит: d = √((x₂-x₁)² + (y₂-y₁)²), где (x₁, y₁) и (x₂, y₂) - координаты вершин треугольника.
Если у вас есть только длины двух сторон треугольника и угол между ними, вы можете использовать формулу Синуса для вычисления длины диагонали. Формула Синуса гласит: d = (a*sin(B))/sin(A-B), где d - длина диагонали, a - длина одной стороны треугольника, A и B - углы между сторонами и диагональю.
Важно помнить, что для правильного использования этих формул необходимо знать значения углов или длины сторон треугольника. Если вам известны только часть данных, например, две длины сторон и угол между ними, вы можете использовать комбинацию формул для нахождения длины диагонали.
Какой вид диагонали бывает у треугольника?

- Медиана – это диагональ, которая соединяет вершину треугольника с серединой противоположной стороны. В треугольнике всегда существуют три медианы, и они пересекаются в одной точке – центре тяжести треугольника. Центр тяжести является точкой пересечения медиан и является центром равновесия для треугольника.
- Биссектриса – это диагональ, которая делит угол треугольника на два равных угла. У каждого угла треугольника существует по одной биссектрисе, и они пересекаются в точке вписанной окружности треугольника. Вписанная окружность треугольника – это окружность, которая касается всех трех сторон треугольника.
Знание видов диагоналей треугольника помогает в решении задач с использованием треугольной геометрии и зачастую является необходимым для нахождения площадей и других свойств треугольника.
Как вычислить длину диагонали в прямоугольном треугольнике?

Для вычисления длины диагонали в прямоугольном треугольнике используется теорема Пифагора. Эта теорема гласит, что квадрат длины гипотенузы (самой длинной стороны) равен сумме квадратов длин двух других сторон.
Таким образом, если известны длины катетов (двух боковых сторон) прямоугольного треугольника, то можно вычислить длину диагонали при помощи следующей формулы:
Длина диагонали = √(a^2 + b^2)
где a и b - длины катетов прямоугольного треугольника.
Если известны значения длин катетов, достаточно просто возвести их в квадрат, сложить результаты и извлечь квадратный корень из полученной суммы. Полученное число будет являться длиной диагонали треугольника.
Как найти длину диагонали в равнобедренном треугольнике?

Длина диагонали в равнобедренном треугольнике может быть найдена с помощью теоремы Пифагора или выражения, основанного на полуосновании и высоте треугольника.
Выражение для длины диагонали в равнобедренном треугольнике:
| Диагональ | = | √(2 * a^2 - 2 * b^2) |
где a - длина основания (половина основания), b - длина высоты, опущенной на основание.
Используя эту формулу, можно легко вычислить длину диагонали в равнобедренном треугольнике, если известны значения полуоснования и длины высоты.
Формула для нахождения диагонали равнобедренного треугольника
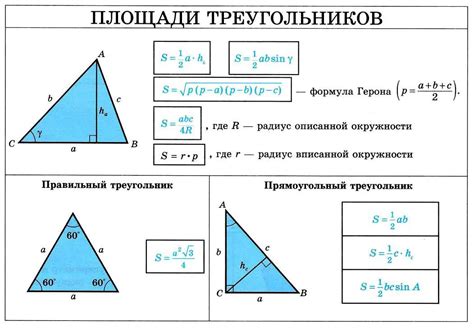
Формула для нахождения диагонали равнобедренного треугольника выглядит следующим образом:
Диагональ = √(2 * a^2 - b^2),
где a – длина основания треугольника,
а b – длина боковой стороны (стороны, равной основанию).
Используя данную формулу, можно легко найти длину диагонали равнобедренного треугольника, зная значения основания и боковой стороны.
Как вычислить длину диагонали в разностороннем треугольнике?

Шаги по вычислению длины диагонали:
- Определите длину каждой стороны треугольника. Используйте формулу расстояния между двумя точками для определения расстояния между каждой парой вершин треугольника.
- Используя закон косинусов, вычислите величину каждого угла треугольника. Закон косинусов гласит: квадрат длины одной стороны равен сумме квадратов длины двух других сторон, умноженных на два произведения этих сторон и косинус соответствующего угла.
- Выберите угол, вершина которого не является одной из точек диагонали.
- Используйте формулу синусов для вычисления длины диагонали. Формула синусов гласит: длина диагонали равна отношению произведения длин двух сторон треугольника к удвоенному синусу угла между этими сторонами.
Применение этих шагов позволит вычислить длину диагонали в разностороннем треугольнике.
Формула для нахождения диагонали разностороннего треугольника
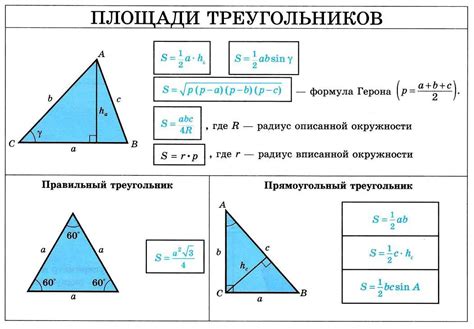
Формула для нахождения диагонали разностороннего треугольника выглядит следующим образом:
d = √(a^2 + b^2 - 2abcosC)
Где:
d - длина диагонали разностороннего треугольника;
a и b - длины сторон треугольника;
C - угол между сторонами a и b.
Эта формула основана на теореме косинусов и позволяет рассчитать длину диагонали треугольника, зная длины его сторон и угол между ними.
Применение этой формулы позволяет точно определить длину диагонали разностороннего треугольника и использовать это знание для решения различных геометрических задач.