Окружности – одни из самых интересных и базовых геометрических фигур. Диаметр окружности играет важную роль в ее изучении и анализе. Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Найти диаметр окружности можно с помощью простой и доступной формулы, а также с использованием различных способов расчета.
Формула для нахождения диаметра окружности основана на соотношении между диаметром (D) и радиусом (r) окружности. Радиус – это отрезок, соединяющий центр окружности с любой точкой на ее окружности. Формула звучит следующим образом: D = 2r. То есть, диаметр окружности равен удвоенному значению радиуса.
Если известно значение радиуса окружности, то можно использовать данную формулу для расчета диаметра. Например, при значении радиуса r = 5 единиц, диаметр окружности будет равен D = 2 * 5 = 10 единиц. Таким образом, диаметр окружности всегда будет в два раза больше радиуса.
Существует и другой способ для нахождения диаметра окружности. Если известна длина окружности (C), то диаметр можно вычислить с помощью формулы: D = C / π. Здесь π (пи) – математическая константа, часто принимаемая равной 3,14 или округленной до двух знаков после запятой (3,1415). Таким образом, имея значение длины окружности, можно найти диаметр.
Определение диаметра окружности
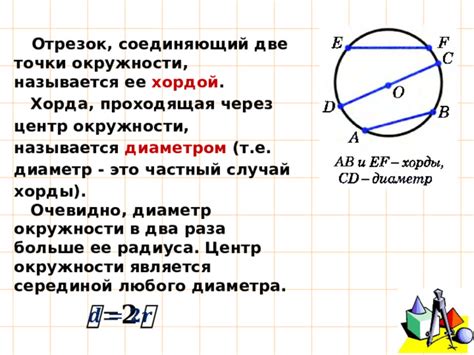
Для определения диаметра окружности существует несколько способов. Один из самых простых способов - измерение диаметра с помощью линейки или штангенциркуля. Для этого необходимо разместить окружность на плоской поверхности и аккуратно измерить расстояние между двумя точками, расположенными на противоположных сторонах окружности. Полученное значение будет равно диаметру окружности.
Еще одним способом определения диаметра окружности является использование формулы, связывающей диаметр с радиусом окружности. Радиус окружности - это расстояние от ее центра до любой точки на окружности. Формула для рассчета диаметра окружности выглядит следующим образом:
d = 2r
где d - диаметр, r - радиус окружности.
Таким образом, зная значение радиуса окружности, можно легко вычислить ее диаметр, просто удвоив радиус.
Определение диаметра окружности имеет большое практическое значение в различных областях, таких как геометрия, инженерия, архитектура и др. Расчет диаметра позволяет определить размеры и форму объектов, основанных на окружностях, и является неотъемлемым элементом при проектировании и изготовлении различных изделий и конструкций.
Формула для расчета диаметра

Для вычисления диаметра окружности существует простая формула: диаметр равен двум радиусам или дважды больше радиуса. Математический символ для обозначения диаметра – D.
Таким образом, если радиус окружности равен R, то диаметр можно выразить следующей формулой:
D = 2R
Например, если радиус окружности равен 5 см, то диаметр будет равен:
D = 2 * 5 = 10 см
Формула для расчета диаметра является простым и удобным инструментом, который часто используется в геометрии и других областях науки и техники.
Не забывайте, что диаметр окружности является одним из основных параметров, которые могут быть использованы для вычисления других характеристик окружности, например, ее площади или длины окружности.
Метод 1: Использование длины окружности

Если известна длина окружности, то диаметр можно вычислить по формуле:
d = C / π
где d - диаметр, C - длина окружности, π - математическая константа "пи", примерное значение которой равно 3,14159.
Чтобы найти диаметр окружности, необходимо знать длину окружности. Длину окружности можно измерить с помощью ленты или шнурка, обернутого вокруг окружности. Если длина окружности известна, то можно использовать данную формулу для получения значения диаметра.
- Замерьте длину окружности с помощью ленты или шнурка. Оберните его вокруг окружности, чтобы определить точное значение длины.
- Запишите полученное значение длины окружности.
- Воспользуйтесь формулой d = C / π, чтобы вычислить диаметр окружности.
- Подставьте известное значение длины окружности в формулу и выполните вычисления. Полученный результат будет являться значением диаметра.
Теперь вы знаете, как вычислить диаметр окружности, используя формулу, основанную на длине окружности. Этот метод может быть полезен при работе с реальными объектами или в задачах, связанных с геометрией и дизайном.
Метод 2: Вычисление по площади круга

Если известна площадь круга, можно вычислить его диаметр с использованием специальной формулы. Данная формула основывается на том факте, что площадь круга связана с его радиусом следующим образом:
S = πr²
где S - площадь круга, а r - радиус.
Чтобы найти диаметр круга, нужно провести серединный перпендикуляр к его радиусу. Зная, что диаметр равен удвоенному значению радиуса (d = 2r), можно выразить радиус через диаметр:
r = d/2
Теперь остается только подставить это выражение в формулу для площади:
S = π(d/2)²
Тогда выражение для диаметра в зависимости от площади будет следующим:
d = √(4S/π)
Где d - диаметр круга, а S - площадь.
Таким образом, если известна площадь круга, можно легко вычислить его диаметр, используя данную формулу.
Примеры расчетов диаметра
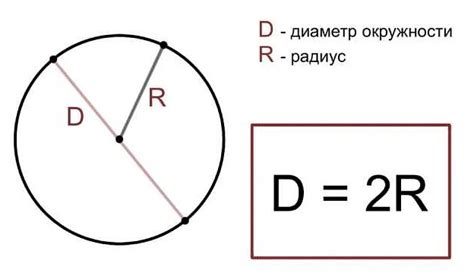
Рассмотрим несколько примеров расчета диаметра окружности при известной длине окружности или площади круга.
Пример 1:
Пусть известна длина окружности равна 20 см. Найдем диаметр окружности.
Используем формулу: d = L / π, где d - диаметр окружности, L - длина окружности, а π (пи) - математическая константа, примерно равная 3.14159.
Подставляем известные значения: d = 20 / 3.14159 ≈ 6.37
Таким образом, диаметр окружности примерно равен 6.37 см.
Пример 2:
Пусть известна площадь круга равна 50 квадратных см. Найдем диаметр окружности.
Используем формулу: d = √(4S / π), где d - диаметр окружности, S - площадь круга, а π (пи) - математическая константа, примерно равная 3.14159.
Подставляем известные значения: d = √(4 * 50 / 3.14159) ≈ √(200 / 3.14159) ≈ √(63.66) ≈ 7.98
Таким образом, диаметр окружности примерно равен 7.98 см.
Пример 3:
Пусть известна площадь круга равна 100 квадратных см. Найдем диаметр окружности.
Используем формулу: d = √(4S / π), где d - диаметр окружности, S - площадь круга, а π (пи) - математическая константа, примерно равная 3.14159.
Подставляем известные значения: d = √(4 * 100 / 3.14159) ≈ √(400 / 3.14159) ≈ √(127.32) ≈ 11.29
Таким образом, диаметр окружности примерно равен 11.29 см.