Радиус и хорда сектора - важные параметры, которые позволяют нам оценить его размер и форму. Однако, если нам нужно найти длину дуги этого сектора, то нам понадобятся дополнительные вычисления. Существует простой способ расчета этого значения, который не требует сложных формул или математических операций.
Для начала, нам необходимо знать значение радиуса и длины хорды сектора. Радиус представляет собой расстояние от центра до края сектора, а хорда - отрезок, соединяющий две точки на окружности сектора. Оба эти значения должны быть известны, чтобы продолжить вычисления.
Длина дуги сектора можно найти с помощью следующей формулы:
длина дуги = (длина хорды * 2 * радиус * π) / 360
Где π (или пи) - это математическая константа, приближенное значение которой равно 3.14159. Оно используется для выражения отношения длины окружности к ее диаметру.
Используя эту простую формулу, вы сможете легко найти длину дуги сектора при известных значениях радиуса и хорды. Это позволит вам точно определить размер и форму данного сектора и использовать эти значения для дальнейших вычислений. Необходимо отметить, что величина угла сектора не учитывается в этой формуле, так как для нахождения длины дуги сектора она не является необходимой.
Как найти длину дуги сектора?
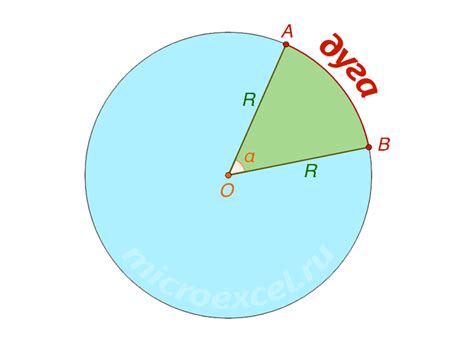
Для нахождения длины дуги сектора с известным радиусом и хордой можно воспользоваться простой формулой:
Длина дуги сектора = (хорда * 2π * радиус) / (2 * площади полной окружности)
Для использования этой формулы необходимо знать радиус и хорду сектора. Радиус – это расстояние от центра окружности до любой точки на окружности, а хорда – это отрезок, соединяющий две точки на окружности.
Давайте рассмотрим пример. Предположим, у нас есть окружность радиусом 5 см и хорда, равная 4 см. Как найти длину дуги сектора?
| Данные | Значения |
|---|---|
| Радиус (r) | 5 см |
| Хорда (c) | 4 см |
Для начала посчитаем площадь полной окружности:
Площадь полной окружности = π * (радиус^2)
Площадь полной окружности = π * (5^2) = 25π кв.см
Теперь воспользуемся формулой для нахождения длины дуги сектора:
Длина дуги сектора = (хорда * 2π * радиус) / (2 * площади полной окружности)
Длина дуги сектора = (4 * 2π * 5) / (2 * 25π)
Длина дуги сектора = (40π) / (50π)
Длина дуги сектора = 0.8 * 2π * радиус
Таким образом, длина дуги сектора равна 0.8 радиуса окружности.
Это простой способ расчета длины дуги сектора с известным радиусом и хордой. Учитывайте, что результат будет выражен в тех же единицах длины, что и радиус окружности.
Простой способ расчета

Для расчета длины дуги сектора с известным радиусом и хордой существует простой способ.
1. Найдите угол α, который образуют хорда и радиус. Для этого можно воспользоваться тригонометрическим соотношением: α = 2arcsin(х/2r), где х - длина хорды, r - радиус сектора.
2. После того как угол α найден, можно использовать формулу для нахождения длины дуги. Формула выглядит следующим образом: L = αr, где L - длина дуги, α - угол в радианах, r - радиус сектора.
Таким образом, для расчета длины дуги сектора с известным радиусом и хордой необходимо найти угол α, используя тригонометрическое соотношение, а затем умножить его на радиус сектора.
Этот простой способ расчета позволяет быстро и без лишних сложностей определить длину дуги сектора по известным параметрам - радиусу и хорде.
Известный радиус и хорда
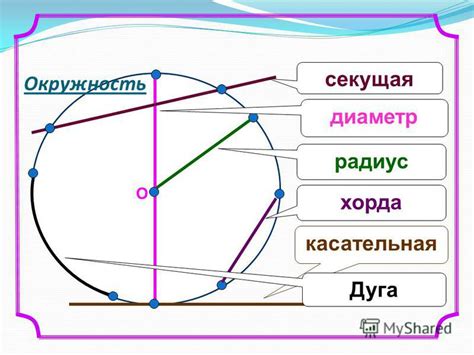
Найти длину дуги сектора с известным радиусом и хордой можно с помощью несложной математической формулы, которая позволяет точно определить данное значение.
Для этого необходимо знать длину радиуса (R) и длину хорды (l). Сначала находим центральный угол (α), используя формулу α = 2 * arcsin (l / 2R). Затем, с помощью формулы s = αR, где s - искомая длина дуги сектора, находим значение искомой длины.
Если известны радиус и хорда, то данный метод позволяет с легкостью определить длину дуги сектора без необходимости проводить измерения или использовать сложные вычисления.