Геометрия всегда была сложной для многих студентов. Все эти многоугольники, треугольники, прямые линии - иногда кажется, что в этом каше невозможно разобраться. Но не стоит отчаиваться! Сегодня мы расскажем вам о методе, который поможет вам найти длину гипотенузы через биссектрису треугольника. Захотите ли вы стать геометрическим гением или просто успешно справиться с домашним заданием - этот подробный гайд с примерами поможет вам разобраться в этой теме лучше.
Прежде чем мы продолжим, важно понимать, что биссектриса треугольника - это прямая, которая делит внутренний угол треугольника пополам. Важность биссектрисы заключается в том, что она играет важную роль в нахождении длины гипотенузы. К счастью, расчет длины гипотенузы через биссектрису не является сложным процессом.
Давайте рассмотрим пример, чтобы лучше понять этот процесс. Представим, что у нас есть прямоугольный треугольник, у которого известны две стороны, а также длина биссектрисы, проведенной к гипотенузе. Мы можем использовать эти данные, чтобы найти длину гипотенузы с помощью простой формулы. Удивительно, правда?
Что такое биссектриса? Определение и основные свойства

Основные свойства биссектрисы:
| 1. Каждая биссектриса перпендикулярна к соответствующей стороне треугольника. |
| 2. Точка пересечения биссектрис треугольника называется центром вписанной окружности этого треугольника. |
| 3. Биссектриса делит противоположный ей угол на две равные части. |
| 4. Биссектриса равноудалена от сторон угла, которые она делит. |
Знание свойств биссектрисы позволяет упростить решение задач на геометрию и дает возможность находить значения различных величин, включая длину гипотенузы через биссектрису.
Начальные понятия: угол и биссектриса
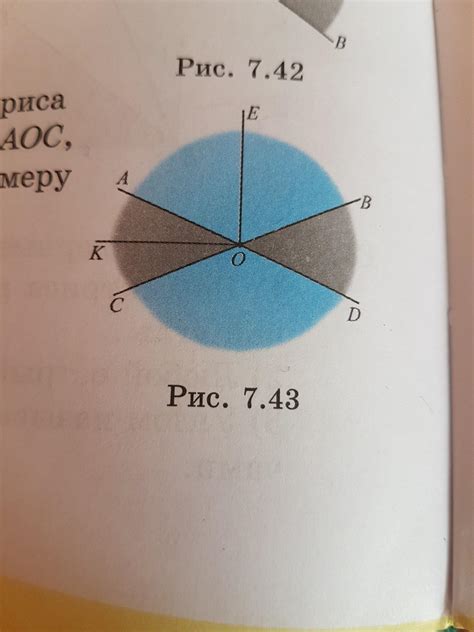
- Угол: это фигура, образованная двумя лучами, которые начинаются из одной точки, называемой вершиной угла. Углы в геометрии могут быть различной величины и классифицируются в зависимости от своей величины. Угол может быть острый, прямой, тупой или полный (сумма всех углов в плоской фигуре).
- Биссектриса: биссектрисой угла называется прямая или луч, которая делит данный угол на два равных угла. Биссектриса проходит через вершину угла и делит его на две части.
Понимание этих основных понятий является ключевым для понимания метода нахождения длины гипотенузы через биссектрису. Действуя согласно правилам геометрии и использованию биссектрисы можно решить различные задачи и вычисления, включая нахождение длины гипотенузы.
В следующих разделах мы более подробно рассмотрим этот метод и предоставим примеры его применения.
Теорема о биссектрисе и ее применение
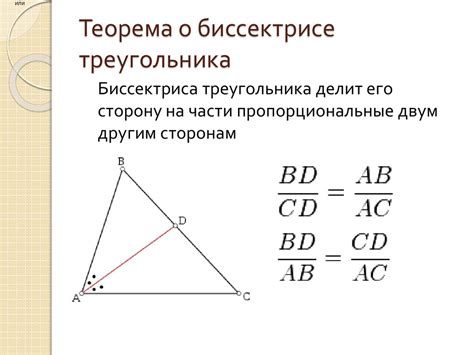
Теорема о биссектрисе можно записать следующим образом:
Если в треугольнике ABC B:
BD – биссектриса угла BAC, AC – противолежащая сторона, AB и BC – другие две стороны, то:
AB/BC = AC/BD
Эта теорема является важным инструментом в геометрии и применяется для решения различных задач, в том числе и для нахождения длины гипотенузы через биссектрису. Зная длины биссектрисы и противолежащей ей стороны, можно определить длину других сторон треугольника.
Знание теоремы о биссектрисе позволяет выполнять сложные геометрические конструкции, находить углы и длины сторон треугольников, а также решать разнообразные задачи по определению площадей и объемов фигур. Эта теорема является одним из ключевых элементов обучения геометрии и находит применение в различных областях науки и техники.
Формула для нахождения длины биссектрисы
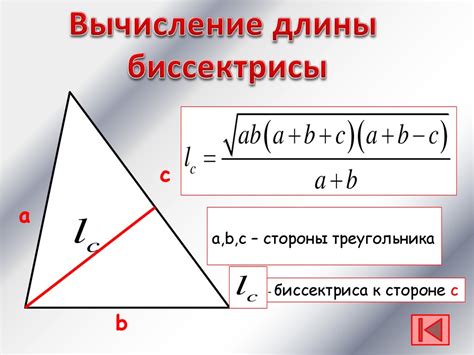
Существует формула, которая позволяет найти длину биссектрисы исходя из длин сторон треугольника. Формула выглядит следующим образом:
Длина биссектрисы B равна произведению квадратного корня из произведения длин двух сторон треугольника на косинус половины внутреннего угла между этими сторонами. То есть:
B = 2 * sqrt(p * (p - a) * (p - b) * (p - c)) / (b + c),
где a, b и c – длины сторон треугольника, а p – полупериметр (p = (a + b + c) / 2).
Эта формула основана на теореме о биссектрисе треугольника, которая утверждает, что биссектриса делит соответствующую сторону треугольника пропорционально другим двум сторонам.
Способы нахождения длины гипотенузы через биссектрису

Существуют два способа нахождения длины гипотенузы через биссектрису:
| Способ | Описание |
|---|---|
| Способ 1 | Использование теоремы синусов. |
| Способ 2 | Использование свойств биссектрисы треугольника. |
Способ 1: Использование теоремы синусов
Если известны длины сторон, пересекаемых биссектрисой, и угол между этими сторонами, мы можем использовать теорему синусов, чтобы найти длину гипотенузы. Формула для этого способа следующая:
a / sin(A) = h / sin(C)
где a - длина одной из сторон, пересекаемых биссектрисой, A - угол между этими сторонами, h - длина гипотенузы, C - угол противолежащий гипотенузе.
Способ 2: Использование свойств биссектрисы треугольника
Если известны длины обеих сторон, пересекаемых биссектрисой, мы можем использовать свойства биссектрисы треугольника. Формула для этого способа следующая:
h = 2 * a * b / (a + b)
где a и b - длины сторон, пересекаемых биссектрисой, h - длина гипотенузы.
Теперь у вас есть два способа нахождения длины гипотенузы через биссектрису. Выберите тот, который вам удобнее и применяйте его в своих расчётах!
Способ 1: использование теоремы Пифагора

Для того чтобы найти длину гипотенузы через биссектрису, мы можем использовать знаменитую теорему Пифагора. Эта теорема утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин двух катетов.
Итак, допустим у нас есть треугольник ABC, где AB - гипотенуза, BC - биссектриса треугольника, и AC и AC - катеты. Мы хотим найти длину гипотенузы AB.
Сначала нам нужно найти длину катетов AC и BC. Это можно сделать, используя свойства биссектрисы. Например, мы можем использовать формулу:
AC = (2 * b * c) / (b + c), где b и c - длины отрезков, на которые биссектриса BC делит сторону AB на две части.
Затем мы можем использовать теорему Пифагора для нахождения длины гипотенузы AB:
AB = √(AC^2 + BC^2)
Итак, используя данные о биссектрисе и теореме Пифагора, мы можем найти длину гипотенузы треугольника через биссектрису.
Способ 2: применение тригонометрических функций
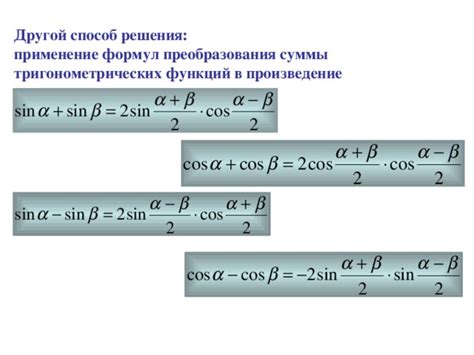
Существует еще один способ определения длины гипотенузы через биссектрису, который основан на использовании тригонометрических функций.
Для использования этого метода необходимо знать значение одного из углов треугольника. Обозначим этот угол через α.
Сначала найдем длины катетов треугольника, используя тригонометрические функции и известную длину биссектрисы. Пусть биссектриса равна b, а длины катетов – a и c соответственно.
Зная, что биссектриса делит угол α на два равных угла, можем использовать тригонометрическую функцию тангенс для определения соотношения длин катетов к биссектрисе:
- tan(α/2) = a/b
- a = b * tan(α/2)
Аналогично, используя тригонометрические функции, можем определить соотношение длин катетов и гипотенузы:
- sin(α) = a/c
- c = a / sin(α)
Теперь, найдя длины катетов a и c, можно вычислить длину гипотенузы h с помощью теоремы Пифагора:
- h^2 = a^2 + c^2
- h = sqrt(a^2 + c^2)
Таким образом, применение тригонометрических функций позволяет нам определить длину гипотенузы треугольника через биссектрису и известный угол α.
Примеры решения задач на нахождение длины гипотенузы через биссектрису

Ниже приведены несколько примеров задач, в которых требуется найти длину гипотенузы через биссектрису:
- Пример 1:
- Пример 2:
- Пример 3:
Рассмотрим треугольник ABC, в котором угол B равен 90 градусов. Биссектриса угла B делит сторону AC на две части, AB и BC. Известно, что AB = 6 см, а BC = 8 см. Найдем длину гипотенузы AC.
Решение:
Используя теорему Пифагора, длина гипотенузы AC может быть найдена по формуле AC = sqrt(AB^2 + BC^2). В данном случае, AC = sqrt(6^2 + 8^2) = sqrt(36 + 64) = sqrt(100) = 10 см.
Рассмотрим треугольник DEF, в котором угол E равен 90 градусов. Биссектриса угла E делит сторону DF на две части, DE и EF. Известно, что DE = 5 см, а EF = 12 см. Найдем длину гипотенузы DF.
Решение:
Используя теорему Пифагора, длина гипотенузы DF может быть найдена по формуле DF = sqrt(DE^2 + EF^2). В данном случае, DF = sqrt(5^2 + 12^2) = sqrt(25 + 144) = sqrt(169) = 13 см.
Рассмотрим треугольник GHI, в котором угол H равен 90 градусов. Биссектриса угла H делит сторону GH на две части, GI и IH. Известно, что GI = 9 см, а IH = 15 см. Найдем длину гипотенузы GH.
Решение:
Используя теорему Пифагора, длина гипотенузы GH может быть найдена по формуле GH = sqrt(GI^2 + IH^2). В данном случае, GH = sqrt(9^2 + 15^2) = sqrt(81 + 225) = sqrt(306) ≈ 17.5 см.
Таким образом, приведенные выше примеры показывают, как использовать биссектрису в задачах на нахождение длины гипотенузы треугольника.