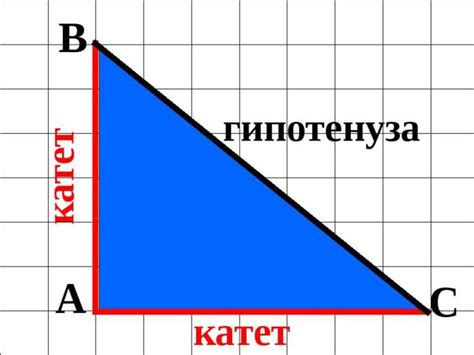
Геометрия – одна из сфер науки, которая является основой многих других дисциплин. Она позволяет изучать формы и отношения между ними. Одной из важных концепций геометрии является прямоугольный треугольник. В таком треугольнике особенно важны его стороны, катеты – это они являются прилежащими прямоугольников, а гипотенуза – это его диагональ. Одна из наиболее распространенных задач – найти длину катета, если известна длина другого катета и угол между ними. Если ты интересуешься геометрией и хочешь узнать, как решить эту задачу, то тебе повезло – мы дадим тебе объяснение и примеры.

Для нахождения длины катета с известными катетом и углом необходимо применить тригонометрию. В данной задаче используется тангенс угла. Тангенс – это отношение противолежащего катета к прилегающему. Формула для нахождения длины катета выглядит следующим образом: катет = известный катет / тангенс угла.

Рассмотрим пример для лучшего понимания. Предположим, что в прямоугольном треугольнике один катет равен 5 см, а угол между катетами равен 30 градусов. Чтобы найти второй катет, мы можем использовать вышеуказанную формулу. Подставим значения в нее: катет = 5 / тангенс 30 градусов. Теперь остается только найти значение тангенса 30 градусов. Если мы посмотрим в таблицу тангенсов, то увидим, что его значение равно 0.577. Тогда катет = 5 / 0.577, что дает нам примерно 8.66 см. Таким образом, второй катет равен примерно 8.66 см.

Известны лишь катет и угол: как найти второй катет?

Формула для нахождения катета выглядит следующим образом:

катет = гипотенуза * тангенс(угол)

Сначала нужно найти значение тангенса угла с помощью калькулятора или таблицы значений тангенса, а затем подставить его в формулу вместе с длиной гипотенузы. Умножение даст значение второго катета.

Например, если известны длина одного катета, равная 5 единицам, и угол между этим катетом и гипотенузой, равный 30 градусам, можно найти второй катет следующим образом:

катет = 5 * тангенс(30)

После рассчета значения тангенса угла 30 градусов и его умножения на длину гипотенузы, можно получить значение второго катета.

Теперь вы знаете, как найти значение второго катета в прямоугольном треугольнике, когда известны только длина одного катета и угол между ним и гипотенузой. Эта формула может быть полезной при решении задач на геометрию и в других предметах, где применимы треугольники.

Определение формулы нахождения катета с известными параметрами

Для нахождения значения катета с известными параметрами, необходимо использовать три ингредиента: известный катет, известный угол, и основная формула тригонометрии.

Одна из самых распространенных формул для нахождения катета - это формула синуса. В соответствии с этой формулой:

sin(α) = противолежащий катет / гипотенуза

где α - известный угол, противолежащий катет - катет, который мы хотим найти, и гипотенуза - другой катет, известный нам.

Мы можем переписать эту формулу, чтобы выразить противолежащий катет:

противолежащий катет = sin(α) * гипотенуза

Таким образом, мы можем использовать эту формулу, чтобы найти значение противолежащего катета, используя известный угол и гипотенузу.

Для лучшего понимания формулы, рассмотрим пример:

Пример 1:

У нас есть прямоугольный треугольник, у которого известный катет равен 3, гипотенуза равна 5, и известный угол α составляет 30 градусов. Чтобы найти противолежащий катет, мы можем использовать формулу синуса:

противолежащий катет = sin(30°) * 5

противолежащий катет = 0.5 * 5

противолежащий катет = 2.5

Таким образом, противолежащий катет равен 2.5.

Помните, что формулы для нахождения катета могут различаться в зависимости от известных параметров и используемого тригонометрического отношения. Важно использовать соответствующую формулу и правильно ориентироваться в треугольнике для правильного использования формулы.

Пример решения задачи по нахождению катета с известными параметрами

Предположим, что нам известен один катет треугольника и угол между этим катетом и гипотенузой. Наша задача состоит в том, чтобы найти второй катет треугольника.

Для начала обозначим известные параметры. Пусть a - известный катет, b - неизвестный катет, и C - угол между катетом a и гипотенузой.

Для решения этой задачи мы будем использовать тригонометрическую функцию синуса. Формула для нахождения катета с известными катетом и углом выглядит следующим образом:

b = a * sin(C)

Теперь рассмотрим пример:

Пусть известен катет a = 5 и угол C = 30 градусов. Подставим эти значения в формулу:

b = 5 * sin(30)

Выполняем вычисления:

b = 5 * 0.5

b = 2.5

Ответ: второй катет треугольника равен 2.5.

Зачем нужно уметь находить катет с известными параметрами?

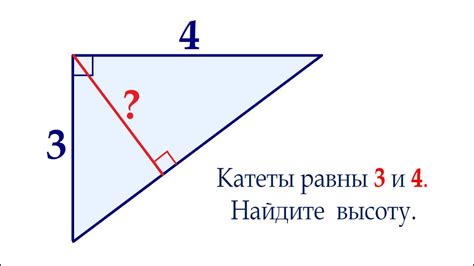
Зная длину одного катета и величину угла между катетами, можно определить длину другого катета. Это позволяет проводить расчеты, строить графики, прогнозировать и анализировать различные явления.

Например, в физике знание длины катета может понадобиться при решении задач связанных с рассеянием света, прямолинейным движением, электрическими цепями и другими явлениями. В астрономии, зная длину катета, можно определить расстояние или размеры небесных тел. В инженерии и конструировании, знание катета необходимо при расчете строений, прогнозировании прочности и т.д.

Умение находить катеты с известными параметрами позволяет ученным, инженерам и другим специалистам решать задачи эффективно и точно. Также, понимание принципа нахождения катета с известными параметрами помогает углубить знания в геометрии и развить логическое мышление.

Особенности применения формулы для нахождения катета с известными параметрами

Формула для нахождения катета с известными параметрами применяется в геометрии для вычисления длины одного из катетов прямоугольного треугольника, если известны длины второго катета и угла между ними.

Основная формула для нахождения катета с известными параметрами выглядит следующим образом:

a = b * tg(φ),

где a - искомый катет, b - известный катет, φ - известный угол, и tg(φ) - тангенс угла φ.

Данная формула основана на тригонометрическом соотношении между катетами и углом в прямоугольном треугольнике. Применяя данную формулу, можно вычислить длину катета, зная длину другого катета и значение угла между ними.

Примером применения формулы может быть следующая ситуация: известны длина одного из катетов, равная 5 единицам длины, и угол между катетами, равный 30 градусам. Подставляя данные в формулу, получаем:

a = 5 * tg(30°) ≈ 2.88.

Таким образом, длина искомого катета составляет примерно 2.88 единицы длины.

Применив данную формулу, можно с легкостью вычислить длину катета прямоугольного треугольника при известном значении другого катета и угла между ними.

Практические примеры использования формулы нахождения катета

1. Пример 1: Нахождение длины катета, если известны другой катет и угол между ними.

   Пусть у нас есть прямоугольный треугольник ABC, где BC - гипотенуза, AC - известный катет, а угол BAC - известный угол.

   Мы знаем, что косинус угла BAC равен отношению длины катета AC к гипотенузе BC:

   cos(BAC) = AC / BC

   Выражая AC через BC, получаем:

   AC = BC * cos(BAC)

   Таким образом, мы можем найти длину катета AC, если известны длина гипотенузы BC и угол BAC.

2. Пример 2: Решение задачи с использованием теоремы Пифагора.

   Пусть у нас есть прямоугольный треугольник XYZ, где YZ и XZ - катеты, а XY - гипотенуза.

   Если мы знаем длины гипотенузы и одного из катетов, мы можем найти длину второго катета с использованием теоремы Пифагора:

   XZ^2 = XY^2 - YZ^2

   Выражая YZ^2 через XY^2 и XZ^2, получаем:

   YZ^2 = XY^2 - XZ^2

   Затем извлекаем квадратный корень и получаем длину катета YZ. Таким образом, мы можем решить задачу, если известны длина гипотенузы и одного из катетов.

3. Пример 3: Решение задачи на нахождение угла между катетом и гипотенузой.

   Пусть у нас есть прямоугольный треугольник PQR, где QR - гипотенуза, PQ - катет, а PR - известный катет.

   Тогда мы можем найти угол QPR с использованием тригонометрической функции синус:

   sin(QPR) = PQ / QR

   Выражая PQ через QR и sin(QPR), получаем:

   PQ = QR * sin(QPR)

   Таким образом, мы можем найти длину катета PQ, если известны длина гипотенузы QR и угол QPR.

Все эти примеры демонстрируют, как использовать формулу нахождения катета по известному катету и углу для решения различных задач с треугольниками.

Нахождение катета: рекомендации и советы

Нахождение катета треугольника может быть важной задачей при решении геометрических задач. Если у вас есть известный катет и угол, то существуют специальные формулы, которые помогут вам найти второй катет.

Одна из таких формул называется "формула нахождения катета по известному катету и углу". Для использования этой формулы, вам понадобится знать длину одного из катетов и величину угла между этим катетом и гипотенузой.

Когда вы используете формулы для нахождения катета, помните, что углы обычно выражаются в радианах, поэтому не забывайте преобразовывать градусы в радианы при необходимости.

Теперь, когда вы знаете формулу и примеры, вы можете использовать этот метод для нахождения катета в различных геометрических задачах. Он отлично подходит для нахождения катета, когда известен другой катет и угол.