Прямоугольный треугольник - это особый вид треугольника, у которого один из углов равен 90 градусам. Важными элементами прямоугольного треугольника являются его стороны, которые называются катетами, и гипотенуза, наибольшая из сторон.
Если у вас есть информация о значении одного из катетов или гипотенузы, вы можете использовать специальные формулы для нахождения значений других сторон. Нахождение катета треугольника очень полезно при решении различных задач в геометрии, строительстве, физике и других областях.
Формула нахождения катета треугольника основана на теореме Пифагора, которая утверждает, что сумма квадратов катетов равна квадрату гипотенузы. Если вы знаете длину гипотенузы и другого катета, то можете воспользоваться формулой для нахождения значения недостающего катета.
Как найти катет прямоугольного треугольника
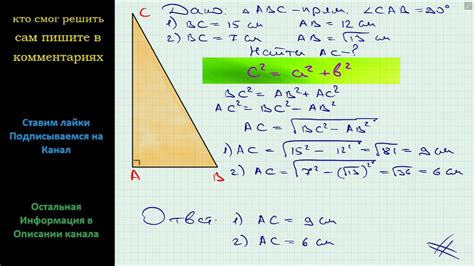
Для нахождения катета прямоугольного треугольника можно использовать формулу гипотенузы и другого катета. Гипотенуза – это сторона треугольника, противоположная прямому углу, а катеты – стороны, прилегающие к прямому углу.
Формула гипотенузы и катета выглядит следующим образом:
Z^2 = X^2 + Y^2
где Z – гипотенуза, а X и Y – катеты.
Если известно значение гипотенузы и одного из катетов, то с помощью данной формулы можно найти второй катет. Для этого нужно из формулы изолировать неизвестный катет и решить полученное уравнение.
Также можно использовать теорему Пифагора для нахождения катета прямоугольного треугольника. Теорема Пифагора гласит, что квадрат гипотенузы равен сумме квадратов катетов:
Z^2 = X^2 + Y^2
Используя данную теорему, можно найти катет прямоугольного треугольника, если известны значения гипотенузы и другого катета. Для этого нужно из формулы изолировать неизвестный катет и решить полученное уравнение.
Если известны значения сторон треугольника, можно воспользоваться тригонометрическими функциями для нахождения катета. Например, для нахождения катета можно использовать функцию тангенс:
tg(α) = Y / X
где α – угол, противолежащий катету Y. Зная значение угла и один из катетов, можно найти второй катет, решив уравнение.
Таким образом, нахождение катета прямоугольного треугольника возможно с использованием формулы гипотенузы и катета, теоремы Пифагора или тригонометрических функций. В данной статье были приведены основные подходы к решению данной задачи.
Формула гипотенузы и катет

Формула гипотенузы: h = √(a² + b²), где a и b – длины катетов, h – длина гипотенузы.
Формула катета: a = √(h² - b²), или b = √(h² - a²), где a и b – длины катетов, h – длина гипотенузы.
| Гипотенуза h | Катет a | Катет b |
|---|---|---|
| 14.0 | 8.0 | √(h² - a²) = √(14.0² - 8.0²) ≈ 11.7 |
| 10.0 | 6.0 | √(h² - a²) = √(10.0² - 6.0²) ≈ 8.0 |
| 12.0 | √(h² - b²) = √(12.0² - 9.0²) ≈ 5.4 | 9.0 |
Как определить катет прямоугольного треугольника
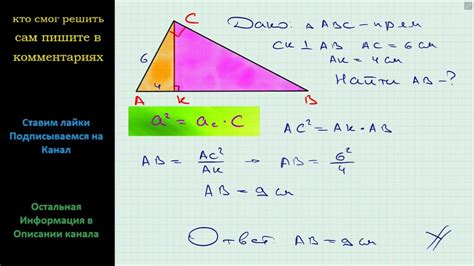
квадрат гипотенузы = квадрат первого катета + квадрат второго катета
Исходя из формулы Пифагора, чтобы найти второй катет, нужно известным значениям гипотенузы и первого катета применить следующий алгоритм:
- Возвести первый катет в квадрат
- Возвести гипотенузу в квадрат
- Вычесть квадрат первого катета из квадрата гипотенузы
- Извлечь квадратный корень из полученного значения
Полученный результат будет представлять собой значение второго катета прямоугольного треугольника. Важно помнить, что для применения данной формулы треугольник должен быть прямоугольным.
Формула для нахождения катета
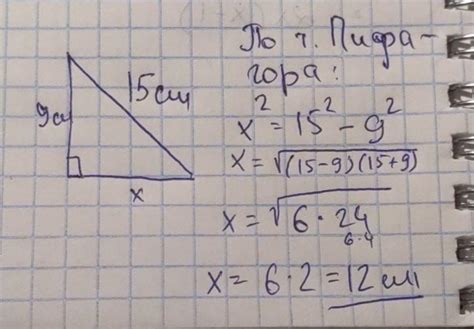
Для нахождения катета прямоугольного треугольника, если известны длина гипотенузы и другого катета, можно использовать следующую формулу:
Катет = √(Гипотенуза² - Другой катет²)
Эта формула основана на теореме Пифагора, которая утверждает, что сумма квадратов катетов равна квадрату гипотенузы.
Чтобы применить эту формулу и найти длину катета, необходимо знать значения гипотенузы и другого катета. Подставьте эти значения в формулу и вычислите катет.
Например, если гипотенуза равна 5 и один из катетов равен 3, то формула будет выглядеть так:
Катет = √(5² - 3²) = √(25 - 9) = √16 = 4
Таким образом, длина катета равна 4.
Как вычислить длину катета прямоугольного треугольника

Катет прямоугольного треугольника – это одна из его сторон, которая перпендикулярна к гипотенузе. Для вычисления длины катета существует знаменитая теорема Пифагора.
Теорема Пифагора утверждает, что квадрат длины гипотенузы треугольника равен сумме квадратов длин его катетов. То есть:
- Для нахождения длины катета, если известна длина гипотенузы и другого катета, нужно вычесть квадрат длины известного катета из квадрата длины гипотенузы, а затем извлечь квадратный корень из полученного значения. Формула для вычисления катета: a = √(c² - b²)
- Для нахождения длины гипотенузы, если известны длины обоих катетов, нужно сложить квадраты длин катетов и затем извлечь квадратный корень из полученной суммы. Формула для вычисления гипотенузы: c = √(a² + b²)
Таким образом, с использованием формулы Пифагора можно легко вычислить длину катета прямоугольного треугольника, если известна длина гипотенузы и другого катета. Эта теорема является важным инструментом в геометрии и находит применение в различных областях науки и техники.
Формула для расчета длины катета
Чтобы найти длину катета, необходимо знать длину гипотенузы и длину другого катета.
Формула для расчета длины катета выглядит следующим образом:
Катет = Корень из квадрата гипотенузы минус квадрат другого катета
Эта формула основана на теореме Пифагора, которая гласит, что квадрат длины гипотенузы равен сумме квадратов длин катетов.
Применение этой формулы позволяет легко и точно рассчитать длину катета в прямоугольном треугольнике.
Пример:
Допустим, у нас есть прямоугольный треугольник, гипотенуза которого равна 10, а второй катет равен 6.
Используя формулу, мы можем рассчитать длину первого катета следующим образом:
Катет = √(10^2 - 6^2) = √(100 - 36) = √64 = 8
Таким образом, длина первого катета равна 8 в данном примере.