Как найти длину медианы прямоугольного треугольника — подробные объяснения и формулы!

Медиана – это линия, соединяющая середину стороны треугольника с противоположним углом. В отличие от медиан обычного треугольника, катеты которого равны между собой, в прямоугольном треугольнике медианы имеют неравные значения. Но как же найти длину медианы в этом случае?

Для того чтобы найти длину медианы прямоугольного треугольника, нужно знать длину его сторон. Назовем стороны треугольника a, b и c, где a и b - катеты, а c - гипотенуза треугольника. Для нахождения медианы, соединяющей середину гипотенузы с противоположным углом, применим формулу:

m = √[(2a² + 2b²) - c²] / 2

В этой формуле m - длина медианы, а √ - знак квадратного корня. С помощью данной формулы легко вычислить длину медианы прямоугольного треугольника, имея значения его сторон. Она основана на теореме Пифагора, которая устанавливает соотношение между сторонами прямоугольного треугольника.

Понятие медианы прямоугольного треугольника

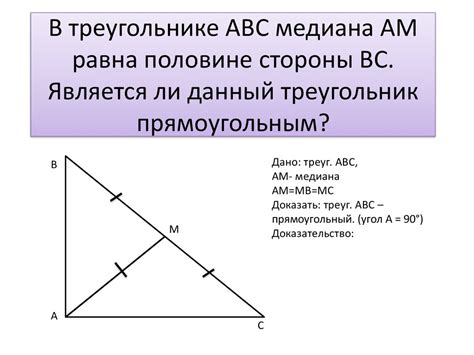
В прямоугольном треугольнике всегда существует три медианы, которые пересекаются в одной точке, называемой центром тяжести или центром масс треугольника. Эта точка делит каждую медиану в отношении 2:1.

Медиана прямоугольного треугольника имеет ряд интересных свойств. Она равна половине диагонали квадрата, вписанного в данный треугольник, и также равна половине длины гипотенузы прямоугольного треугольника.

Медианы прямоугольных треугольников являются важными элементами в геометрии и находят применение в различных задачах и вычислениях. Знание и понимание понятия медианы помогает решать задачи, связанные с треугольниками и их свойствами.

Примечание: В данной статье мы рассматривали медиану прямоугольного треугольника, однако, этот элемент также применяется в других типах треугольников.

Определение и свойства медианы

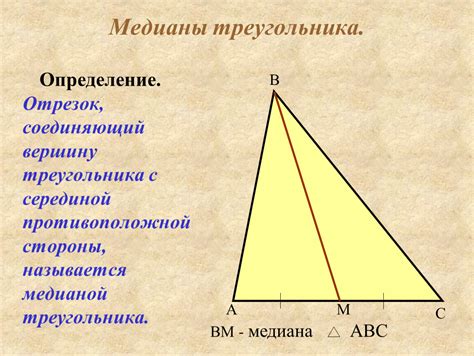
Основное свойство медианы прямоугольного треугольника заключается в том, что она равна половине длины гипотенузы. Это значит, что длина медианы равна половине длины гипотенузы.

Если обозначить длину медианы символом m, а длину гипотенузы - символом c, то свойство медианы можно записать следующим образом:

m = c / 2

То есть, длина медианы равна половине длины гипотенузы.

Это свойство медианы можно использовать для нахождения ее длины при известной длине гипотенузы прямоугольного треугольника.

Применение медианы в геометрии

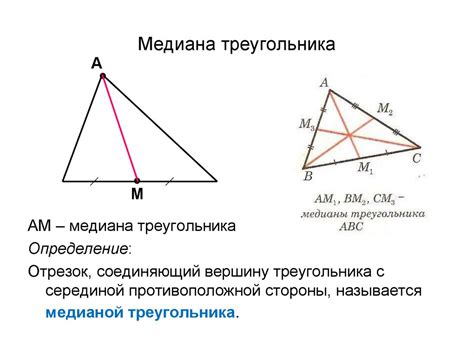
Одним из наиболее распространенных применений медианы является вычисление длины третьей стороны треугольника по длинам двух других сторон. Для этого необходимо знать, что медиана делит прямоугольный треугольник на два равных прямоугольных треугольника, а значит, можно применить теорему Пифагора для нахождения длины медианы.

Между тем, медиана также может служить основой для нахождения площади прямоугольного треугольника. Если известны длины двух из трех сторон треугольника, можно использовать формулу Герона, где медиана выступает в качестве одного из параметров расчета.

Другим применением медианы является определение центра тяжести треугольника. Он находится на пересечении трех медиан и делит каждую из них в отношении 2:1. Центр тяжести является важной характеристикой треугольника и используется при решении множества задач в геометрии и физике.

Таким образом, медиана прямоугольного треугольника играет важную роль в геометрии и находит широкое применение в различных задачах. Она позволяет оценивать длину сторон, находить площадь треугольника и определять его центр тяжести.

Формула для расчета длины медианы

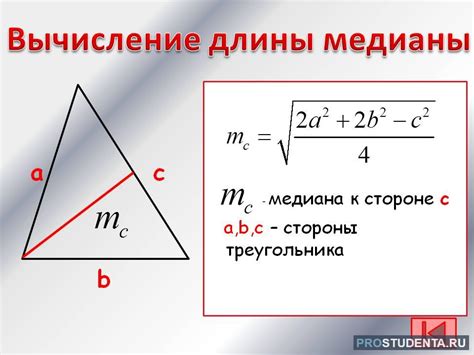
1. Пусть a, b, c - длины сторон прямоугольного треугольника.
2. Найдем длину медианы, проведенной из вершины A к противоположной стороне BC. Обозначим эту медиану как m_a.
3. Используем формулу:

m_a = 0.5 * sqrt(2 * b² + 2 * c² - a²)

Аналогично можно найти длины медиан, проведенных из вершин B и C к противоположным сторонам:

m_b = 0.5 * sqrt(2 * a² + 2 * c² - b²)

m_c = 0.5 * sqrt(2 * a² + 2 * b² - c²)

Используя данные формулы, можно легко вычислить длины медиан прямоугольного треугольника!

Для удобства обозначим длины сторон треугольника следующим образом: AC = a, BC = b и AB = c.

Рассмотрим прямоугольный треугольник BMC. Так как точка M является серединой гипотенузы AC, длина отрезка BM будет равна половине длины гипотенузы. То есть BM = AC/2 = a/2.

Также, прямоугольные треугольники ABC и BMC подобны, так как у них одинаковый угол при вершине B и прямые углы. Из этого следует, что отношение сторон этих треугольников равно: AB/BC = BC/BM.

Подставляя значения сторон треугольника в это равенство, получаем следующую формулу: c/b = b/(a/2).

Для удобства решения, мы можем преобразовать это равенство: c = b^2/(a/2) = 2b^2/a.

Таким образом, мы получаем формулу для нахождения длины медианы BM прямоугольного треугольника: BM = 2b^2/a.

Примеры применения формулы

Давайте рассмотрим несколько примеров, чтобы лучше понять, как использовать формулу для нахождения длины медианы прямоугольного треугольника.

• Пример 1:

  Пусть стороны прямоугольного треугольника равны a = 3, b = 4 и c = 5.

  Найдем длину медианы, опущенной из вершины прямого угла:

  Мы знаем, что медиана, опущенная из вершины прямого угла, равна половине гипотенузы.

  Таким образом, медиана равна:

  M = c/2 = 5/2 = 2.5

• Пример 2:

  Пусть стороны прямоугольного треугольника равны a = 5, b = 12 и c = 13.

  Найдем длину медианы, опущенной из вершины прямого угла:

  Медиана равна половине гипотенузы, поэтому:

  M = c/2 = 13/2 = 6.5

• Пример 3:

  Пусть стороны прямоугольного треугольника равны a = 8, b = 15 и c = 17.

  Найдем длину медианы, опущенной из вершины прямого угла:

  Медиана равна половине гипотенузы, поэтому:

  M = c/2 = 17/2 = 8.5