Медиана - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В равнобедренном треугольнике, у которого две стороны равны, медиана делит основание на две равные части и проходит через точку пересечения высот.
Вычисление длины медианы в равнобедренном треугольнике может быть полезным в геометрии и задачах на построение фигур. Существует простая формула, позволяющая найти длину медианы, если даны значения сторон равнобедренного треугольника.
Для вычисления длины медианы в равнобедренном треугольнике можно воспользоваться формулой: медиана = 0,5 * √(2 * a^2 + 2 * b^2 - c^2), где a и b - стороны треугольника, а c - основание треугольника.
Давайте рассмотрим пример. Пусть у нас есть равнобедренный треугольник со сторонами a = 5 и b = 5, а основание треугольника c = 8. Подставим значения в формулу и произведем вычисления: медиана = 0,5 * √(2 * 5^2 + 2 * 5^2 - 8^2). Рассчитав полученное выражение, мы найдем длину медианы равной 5,66.
Примеры вычисления длины медианы в равнобедренном треугольнике
Для вычисления длины медианы в равнобедренном треугольнике можно использовать специальную формулу. Давайте рассмотрим несколько примеров.
Пример 1:
Пусть у нас есть равнобедренный треугольник ABC, где AB = AC = 6 см, а BC = 8 см. Нам нужно найти длину медианы, проведенной из вершины A.
Сначала найдем длину основания треугольника, которая равна BC = 8 см. Затем мы можем воспользоваться формулой для вычисления длины медианы:
медиана = 0,5 * √(2 * AB^2 + 2 * AC^2 - BC^2)
Подставляя известные значения, получим:
медиана = 0,5 * √(2 * 6^2 + 2 * 6^2 - 8^2)
медиана = 0,5 * √(2 * 36 + 2 * 36 - 64)
медиана = 0,5 * √(72 + 72 - 64)
медиана = 0,5 * √(144 - 64)
медиана = 0,5 * √(80)
медиана ≈ 0,5 * 8,94
медиана ≈ 4,47
Таким образом, длина медианы, проведенной из вершины A в данном равнобедренном треугольнике, приближенно равна 4,47 см.
Пример 2:
Рассмотрим еще один равнобедренный треугольник DEF, где DE = DF = 5 см, а EF = 7 см. Нам нужно вычислить длину медианы, проведенной из вершины D.
Аналогично предыдущему примеру, найдем сначала длину основания треугольника, которая равна EF = 7 см. Затем используем формулу для вычисления длины медианы:
медиана = 0,5 * √(2 * DE^2 + 2 * DF^2 - EF^2)
Подставив известные значения, получим:
медиана = 0,5 * √(2 * 5^2 + 2 * 5^2 - 7^2)
медиана = 0,5 * √(2 * 25 + 2 * 25 - 49)
медиана = 0,5 * √(50 + 50 - 49)
медиана = 0,5 * √(100 - 49)
медиана = 0,5 * √(51)
медиана ≈ 0,5 * 7,14
медиана ≈ 3,57
Таким образом, длина медианы, проведенной из вершины D в данном равнобедренном треугольнике, приближенно равна 3,57 см.
Формула для вычисления длины медианы в равнобедренном треугольнике
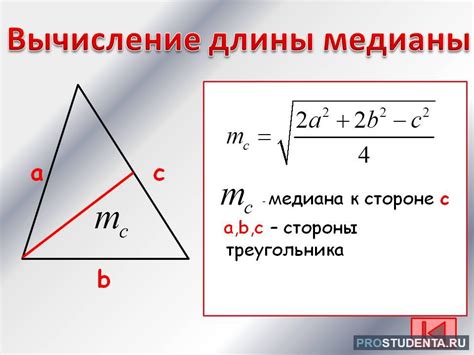
Длина медианы в равнобедренном треугольнике может быть вычислена с использованием формулы:
M = sqrt((2b^2 + a^2)/4)
где M - длина медианы, a - длина длинной стороны треугольника, b - длина короткой стороны треугольника.
Данная формула основана на свойствах равнобедренного треугольника, в котором медиана имеет длину равную половине длины основания треугольника. При вычислении длины медианы необходимо знать длины обеих сторон треугольника.
Таким образом, с использованием данной формулы можно вычислить длину медианы в равнобедренном треугольнике и использовать этот результат для решения различных геометрических задач.