Окружность – это одна из фундаментальных геометрических фигур, которая имеет огромное применение в различных областях науки и техники. Во многих задачах нам часто требуется знать длину окружности, чтобы правильно выполнить расчеты и достичь нужного результата.

Существует формула, позволяющая найти длину окружности, но она может показаться сложной для некоторых людей. Однако, есть и более простые методы, которые помогут без труда определить длину окружности.

Один из таких методов – метод измерения окружности. Для его использования нам понадобятся только линейка и нитка. Просто оберните нитку вокруг окружности и отмерьте полученную длину линейкой. Именно эта величина и будет являться длиной окружности.

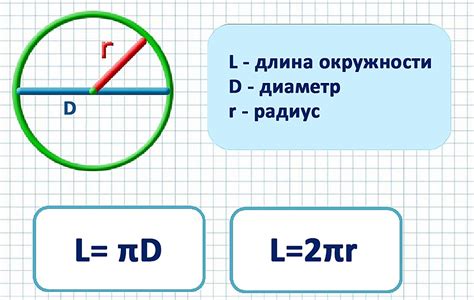
Если у вас нет нитки или вы предпочитаете другой подход, то можно воспользоваться методом измерения диаметра окружности. Диаметр – это отрезок, соединяющий две противоположные точки на окружности, проходящий через ее центр. Если мы знаем диаметр окружности, то длину окружности легко найти, воспользовавшись простым соотношением: длина окружности равна удвоенному значению диаметра, умноженного на число Пи – 3,14.

Методы нахождения длины окружности без формулы:

Однако, существуют и более простые методы нахождения длины окружности без использования формулы. Ниже представлены некоторые из них:

1. Использование линейки или мерной ленты. Самый простой способ - измерить длину окружности с помощью обычной линейки или мерной ленты. Для этого достаточно тщательно измерить расстояние вокруг окружности.
2. Использование шагов. Для аппроксимации длины окружности можно использовать шаги. Необходимо начать от одной точки на окружности и сделать определенное количество шагов вокруг нее. Затем можно измерить длину пути, пройденного за это время, и поделить ее на количество шагов. Таким образом, можно получить приближенное значение длины окружности.
3. Использование тетивы и компаса. Другой способ нахождения длины окружности - использование тетивы и компаса. С помощью компаса можно построить равномерно разделенную окружность, а затем измерить длину тетивы, которая соединяет две точки на окружности. После этого, можно использовать пропорцию между длиной тетивы и длиной окружности для нахождения последней.

Хотя методы без использования формулы могут быть менее точными и требуют дополнительных средств измерения, они все же могут быть полезны в практическом применении, когда точные измерения не так важны.

Геометрический подход

Если у вас есть окружность, можно использовать геометрический подход для определения ее длины. Для этого не требуется использование сложных формул, только элементарные геометрические конструкции.

Первым шагом является измерение радиуса окружности. Зная значение радиуса, можно применить простой метод измерения длины окружности.

Начните с помещения конца измерительной ленты или нити на какую-либо точку на окружности. Затем обведите ленту или нить вокруг окружности так, чтобы она прошла через исходную точку. Пометьте точку, на которой измерительная лента или нить впервые встречается с исходной точкой. Если используете измерительную ленту, просто прочитайте измерение.

Следующим шагом является применение принципа отношения круга к длине окружности. Т.е. длина окружности равна произведению радиуса на два пи. Например, если радиус окружности равен 5 см, длина окружности будет равна 10 пи см или приблизительно 31,4 см.

Используя геометрический подход, можно определить длину окружности без использования сложных формул. Этот метод прост и интуитивно понятен, что делает его доступным для учеников начальных классов и любителей геометрии.

Принцип равенства длин

Для применения принципа, достаточно измерить длину отрезка, который соответствует радиусу окружности. Этот отрезок должен быть равен радиусу, а значит, можно замерить его с помощью линейки или мерного шнура.

После того, как длина радиуса известна, можно просто умножить ее на число π (пи) для расчета длины окружности. Значение числа π равно приближенно 3,14.

Принцип равенства длин прост в использовании и не требует сложных вычислений. Он особенно полезен в ситуациях, когда нет доступа к формулам или вычислительным инструментам.

Компьютерное моделирование

Для моделирования окружности, можно использовать специализированные программы или библиотеки, которые предоставляют готовые инструменты для работы с геометрическими фигурами. Например, можно создать 2D модель окружности и получить ее длину с помощью встроенных функций.

Кроме того, компьютерное моделирование позволяет проводить численные расчеты и анализ окружностей с использованием математических методов. Например, можно использовать метод Монте-Карло для приближенного расчета длины окружности, случайным образом расставляя точки на окружности и вычисляя среднее значение расстояния между ними.

Экспериментальный метод

Если у вас есть физическая модель окружности, вы можете использовать экспериментальный метод для определения ее длины. Для этого вам потребуется нить или ленточка, достаточно длинная, чтобы обернуться вокруг вашей модели окружности.

1. Оберните нить или ленточку вокруг вашей модели окружности так, чтобы она полностью обхватывала ее.

2. Отметьте место, где нить или ленточка пересекается сама с собой. Это место будет вашим измерительным пунктом.

3. Отмотайте нить или ленточку и измерьте расстояние между двумя отметками. Это будет окружность вашей модели.

4. Повторите эксперимент несколько раз, чтобы убедиться в точности измерений.

5. После получения нескольких измерений, вычислите среднюю длину окружности, используя формулу: средняя длина = (сумма всех измерений) / (количество измерений).

Экспериментальный метод может быть полезным способом для приближенного расчета длины окружности, особенно если у вас нет доступа к практичным инструментам и математическим формулам.