Окружность – это геометрическая фигура, представляющая собой замкнутую кривую, все точки которой равноудалены от центра. Окружность является одной из наиболее изучаемых и важных фигур в геометрии, а ее свойства широко применяются в науке, технике и естественных науках.
Если вам требуется найти длину окружности, вы можете использовать специальную формулу, основанную на радиусе окружности. Радиус – это расстояние от центра окружности до любой точки на ее краю. Длина окружности тесно связана с радиусом, и существует простая математическая формула для ее вычисления.
Формула для вычисления длины окружности с помощью радиуса выглядит следующим образом: C = 2πr, где C – длина окружности, π (пи) – математическая константа, приближенно равная 3,14159, и r – радиус окружности.
Давайте рассмотрим пример. Предположим, что у нас есть окружность с радиусом 5 сантиметров. Чтобы вычислить длину окружности, мы используем формулу C = 2πr. Подставляя в нее значение радиуса, получаем C = 2 * 3,14159 * 5 = 31,4159 сантиметров.
Таким образом, длина окружности с радиусом 5 сантиметров составляет приблизительно 31,4159 сантиметров. Эта формула является универсальной и применима для любых значений радиуса окружности. Зная радиус, вы всегда можете легко найти длину окружности, используя эту формулу.
Что такое окружность, и как найти ее длину через радиус?
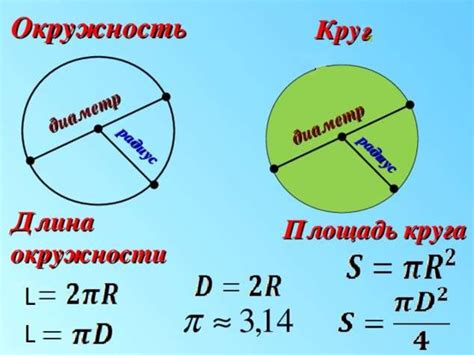
Длина окружности - это расстояние, которое нужно пройти по окружности для полного оборота вокруг центра. Эта длина может быть определена с помощью радиуса окружности.
Формула для нахождения длины окружности через радиус дана постоянной 𝝨, и может быть записана следующим образом:
𝝨 = 2πr
Где:
- 𝝨 - длина окружности
- π (пи) - математическая константа, соответствующая отношению длины окружности к ее диаметру (~3.14159)
- r - радиус окружности
Для вычисления длины окружности через радиус, необходимо знать лишь значение радиуса и применить указанную формулу.
Например, если радиус окружности равен 5 см, то длина окружности будет:
𝝨 = 2π * 5 = 10π см
Таким образом, длина окружности с радиусом 5 см равна 10π см.
Определение и особенности окружности

Окружность имеет ряд особенностей:
| 1 | Диаметр | Отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр является наибольшей возможной хордой окружности. |
| 2 | Радиус | Отрезок, соединяющий центр окружности с любой точкой на окружности. |
| 3 | Хорда | Отрезок, соединяющий две точки на окружности. Хорда может иметь различную длину, но она всегда меньше или равна диаметру окружности. |
| 4 | Сектор | Часть плоскости, ограниченная двумя радиусами и дугой окружности. |
| 5 | Дуга | Часть окружности, ограниченная двумя точками. |
| 6 | Длина окружности | Общая длина дуги окружности. Длина окружности зависит только от ее радиуса и равна произведению радиуса на двойное число пи (π). |
Окружность является одним из основных понятий геометрии и находит широкое применение в различных областях, включая математику, физику и инженерию.
Формула для вычисления длины окружности
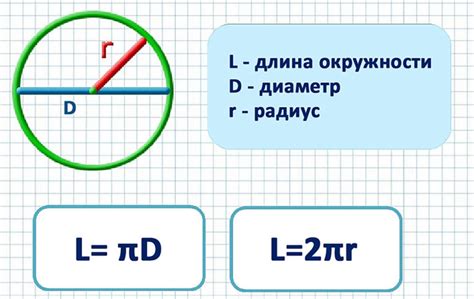
L = 2πr
где r - радиус окружности, а π - математическая константа, приближенно равная 3,14159.
Применение этой формулы особенно полезно, когда нам дан радиус окружности, а мы хотим узнать ее длину. Просто подставьте значение радиуса в формулу и выполните вычисления.
Например, пусть задана окружность с радиусом 5 см. Для нахождения длины окружности нужно умножить радиус на 2π:
L = 2π × 5 = 10π ≈ 31,4159 см.
Таким образом, длина окружности с радиусом 5 см примерно равна 31,4159 см.
Не забывайте, что длина окружности зависит от ее радиуса: чем больше радиус, тем длиннее окружность. Формула позволяет легко и точно вычислить длину окружности с любым заданным радиусом.
Примеры вычисления длины окружности
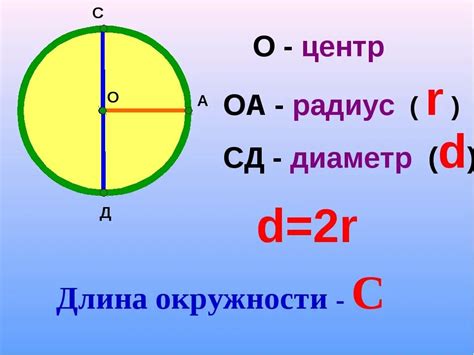
Давайте рассмотрим несколько примеров вычисления длины окружности, используя формулу C = 2πr.
Предположим, что у нас есть окружность с радиусом 5 см.
Чтобы вычислить длину окружности, мы используем формулу: C = 2πr.
Подставляем значение радиуса в формулу: C = 2π * 5.
Вычисляем результат: C = 31.42 см.
Таким образом, длина окружности с радиусом 5 см равна 31.42 см.
Предположим, что у нас есть окружность с радиусом 8 метров.
Снова используем формулу: C = 2πr.
Подставляем значение радиуса в формулу: C = 2π * 8.
Вычисляем результат: C = 50.27 м.
Таким образом, длина окружности с радиусом 8 м равна 50.27 м.
Предположим, что у нас есть окружность с радиусом 2.5 км.
Снова используем формулу: C = 2πr.
Подставляем значение радиуса в формулу: C = 2π * 2.5.
Вычисляем результат: C = 15.71 км.
Таким образом, длина окружности с радиусом 2.5 км равна 15.71 км.
Используя данную формулу, вы можете легко вычислить длину окружности для любого заданного радиуса.
Важные соображения при использовании формулы
При использовании формулы для вычисления длины окружности с помощью радиуса следует учесть несколько важных факторов:
- Единицы измерения: радиус и длина окружности должны быть выражены в одинаковых единицах измерения. Если радиус задан в сантиметрах, то и длина окружности будет выражена в сантиметрах.
- Точность: формула для вычисления длины окружности с помощью радиуса является приближенной. Чем больше число π (пи), которое используется в формуле, тем точнее будет результат. Обычно для расчетов применяется значение π, округленное до двух десятичных знаков (около 3,14).
- Округление: в зависимости от ситуации и требуемой точности, результат может быть округлен до определенного числа десятичных знаков. Например, для использования в инженерных расчетах длина окружности может быть округлена до двух или трех десятичных знаков, а для общего представления результат может быть округлен до одного десятичного знака или выведен без округления.
- Значение пи: значение числа π (пи) является константой и равно примерно 3,14159. Если точное значение π не требуется, можно использовать приближенное значение (3,14), чтобы упростить вычисления и использование формулы.
- Знак длины: в формуле для вычисления длины окружности через радиус, результат будет иметь тот же знак, что и радиус. Например, если радиус отрицательный, то и длина окружности будет отрицательной. Поэтому важно правильно определить знак радиуса при использовании формулы.
С учетом этих важных соображений, формула для вычисления длины окружности через радиус может быть применена с высокой точностью и эффективностью в различных математических и инженерных расчетах.