Окружность – это геометрическая фигура в плоскости, состоящая из всех точек, равноудаленных от фиксированной точки, называемой центром окружности. Размер окружности определяется по ее диаметру, который является отрезком, соединяющим две точки на окружности и проходящим через ее центр. Однако, как найти длину окружности по диаметру?
Формула для нахождения длины окружности по диаметру очень проста. Для этого необходимо умножить диаметр на число π (пи). Математически π не может быть представлено точным числом, однако его значение обычно округляется до 3,14. Таким образом, формула для расчета длины окружности по диаметру будет выглядеть следующим образом:
Длина окружности = Диаметр × π
Также можно использовать другую формулу для нахождения длины окружности, основанную на радиусе окружности. Обратите внимание, что радиус – это половина диаметра. Формула для расчета длины окружности по радиусу будет следующей:
Длина окружности = 2 × радиус × π
Зная длину окружности, можно легко решать задачи геометрии, например, вычислять площадь круга или находить площадь сектора окружности. Расчет длины окружности по диаметру является одним из базовых навыков в геометрии и может быть полезен в различных областях жизни, включая инженерию, архитектуру и строительство.
Что такое диаметр и окружность?

Окружность – это геометрическая фигура, состоящая из всех точек на плоскости, равноудаленных от одной фиксированной точки, называемой центром окружности. Окружность обладает рядом особенностей и свойств, включая длину окружности, которая является одним из основных параметров окружности и может быть рассчитана с использованием диаметра или радиуса окружности.
Диаметр: определение и значение
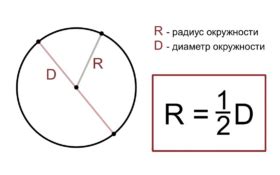
Диаметр имеет большое значение при расчете длины окружности, так как по формуле длины окружности диаметр является исходным параметром. Длина окружности равна произведению диаметра на число π (пи).
Диаметр также используется для определения других характеристик окружности, например, радиуса и площади. Для этого существуют специальные формулы, связывающие диаметр со всеми остальными параметрами окружности.
Знание диаметра окружности позволяет более точно определить ее размеры и использовать его в различных сферах деятельности, включая инженерию, архитектуру, геометрию и физику.
Окружность: основные характеристики

Диаметр окружности определяется как отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Длина диаметра равна удвоенному радиусу окружности.
Радиус окружности - это отрезок, соединяющий центр окружности с любой точкой на окружности. Радиус является половиной диаметра и служит для измерения размеров окружности.
Длина окружности - это периметр, или общая длина окружности. Нахождение длины окружности является важной задачей в геометрии. Для расчета длины окружности используется формула: L = πd, где L - длина окружности, π - математическая константа «пи», а d - диаметр окружности.
Окружности встречаются в различных сферах, таких как геометрия, физика, инженерия и архитектура. Изучение основных характеристик окружности позволяет более глубоко понять и использовать ее свойства и применения.
Формула расчета длины окружности
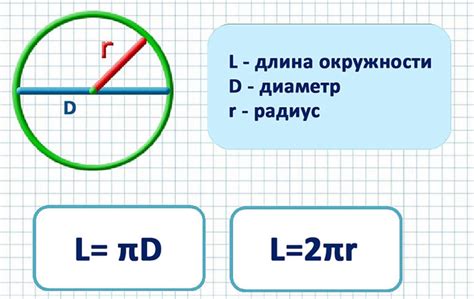
Для расчета длины окружности по диаметру используется следующая формула:
L = π × D
где L - длина окружности, π - математическая константа, равная примерно 3,14159, D - диаметр окружности.
Данная формула позволяет найти длину окружности, зная только ее диаметр. Для расчета необходимо умножить диаметр на число π.
Например, если диаметр окружности равен 10 см, то ее длина будет:
L = 3,14159 × 10 = 31,4159 см
Эта формула является простым и эффективным способом расчета длины окружности по диаметру. Она широко используется в математике, физике, инженерии и других научных областях.
Основная формула: диаметр и число Пи
Формула для расчета длины окружности по диаметру выглядит следующим образом:
L = π * d
где L - длина окружности, d - диаметр окружности.
Для точности расчетов рекомендуется использовать значение числа Пи с большим количеством знаков после запятой. Во многих случаях, приближенное значение π = 3,14159 будет достаточно точным для практических расчетов.
Альтернативные способы расчета

Найдя длину окружности по диаметру с использованием стандартной формулы, можно также применить некоторые альтернативные подходы для получения результата:
- Использование радиуса: длина окружности можно найти, умножив радиус на 2π. Формула будет выглядеть как L = 2πr, где L - длина окружности, r - радиус. Этот метод основывается на связи радиуса и диаметра с помощью формулы d = 2r.
- Геометрический метод: длина окружности можно найти с помощью геометрического подхода. Размер окружности можно приближенно определить, разделив ее на несколько небольших отрезков и измерив их суммарную длину. Чем больше отрезков, тем точнее будет результат.
- Метод использования угла: окружность можно рассматривать в качестве части окружности большего радиуса с углом в 360 градусов. Длину окружности можно найти, используя формулу L = 2πr(θ/360), где θ - угол в градусах. Этот метод пригодится, если необходимо найти длину окружности только для определенного угла.
Все эти способы позволяют найти длину окружности по диаметру с разных точек зрения и могут быть использованы в различных ситуациях в зависимости от задачи или удобства расчета.
Практические примеры: как применить формулу
Теперь, когда мы знаем формулу для расчета длины окружности по диаметру, давайте рассмотрим несколько практических примеров, чтобы лучше понять, как ее применять в реальных задачах.
Пример 1: У нас есть окружность с диаметром 10 см. Какова будет ее длина?
Решение: Для решения этой задачи мы можем использовать формулу для расчета длины окружности по диаметру:
| Диаметр (d) | 10 см |
| Пи (π) | 3.14 (приближенное значение) |
| Длина окружности (C) | π * d |
| Результат | 3.14 * 10 см = 31.4 см |
Таким образом, длина окружности с диаметром 10 см равна 31.4 см.
Пример 2: Нам дана окружность с диаметром 6 м. Какова будет ее длина?
Решение: В этом примере мы также будем использовать формулу для расчета длины окружности по диаметру:
| Диаметр (d) | 6 м |
| Пи (π) | 3.14 (приближенное значение) |
| Длина окружности (C) | π * d |
| Результат | 3.14 * 6 м = 18.84 м |
Итак, длина окружности с диаметром 6 м равна 18.84 м.
Знание формулы для расчета длины окружности по диаметру поможет вам решать различные задачи, связанные с окружностями, например, когда вам необходимо измерить периметр круга или определить, сколько проволоки потребуется для изготовления кольца. Успехов в использовании формулы!