Окружность шара - одна из самых важных геометрических фигур, чьи свойства исследуются уже не одно тысячелетие. Знание длины окружности шара позволяет решать различные задачи в физике, строительстве, архитектуре и других областях науки и техники.
Но как найти длину окружности шара простыми формулами? Для этого можно воспользоваться аналитической и геометрической методиками расчета. Обе эти методики позволяют получить точный результат, но имеют различные подходы к решению задачи.
Аналитический метод расчета заключается в использовании специальной формулы, которая выражает длину окружности через радиус шара. Эта формула известна как формула Лапласа-Пуассона и выглядит следующим образом: L = 2πr, где L - длина окружности, π - число "пи" (примерно равно 3,14159), r - радиус шара. Эта формула проста в использовании и позволяет получить результат быстро и надежно.
Геометрический метод расчета заключается в использовании свойств окружности и треугольника. Основная идея этого метода состоит в разбиении окружности на малые равные участки, вычислении длины каждого участка, а затем суммировании полученных значений. Для этого можно использовать метод умножения длины окружности большого радиуса на соответствующий коэффициент. Например, если известен радиус R, можно найти длину окружности с радиусом r, используя формулу L = (2πR) * (r / R). Этот метод требует некоторых геометрических навыков, но позволяет получить более точный результат при больших значениях радиуса.
Расчет длины окружности шара: простые формулы и методы
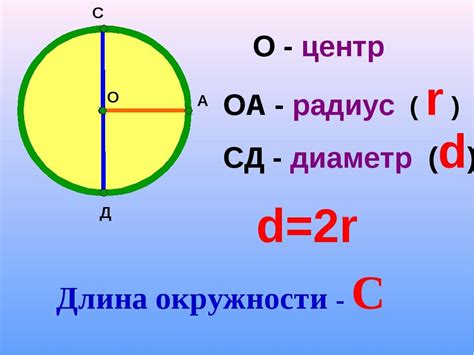
Один из простых способов расчета длины окружности шара - использование радиуса шара (r) и формулы:
C = 2 * π * r
где C - длина окружности, π - математическая константа, примерное значение которой 3.14.
Также можно использовать диаметр шара (d) для расчета длины окружности с помощью формулы:
C = π * d
Для более точного значения длины окружности шара можно использовать выражение:
C = π * d + 2 * (r - d)
где r - радиус шара, d - диаметр шара.
Данные формулы и методы позволяют легко и быстро рассчитать длину окружности шара с помощью простых математических операций. Необходимо только знать значения радиуса или диаметра шара.
| Значение | Формула |
|---|---|
| Длина окружности шара по радиусу | C = 2 * π * r |
| Длина окружности шара по диаметру | C = π * d |
| Длина окружности шара (точное значение) | C = π * d + 2 * (r - d) |
Используя эти простые формулы и методы, вы сможете легко рассчитать длину окружности шара в любой ситуации. Знание длины окружности шара может быть полезным при решении различных геометрических задач или при выполнении технических расчетов.
Формула расчета длины окружности шара
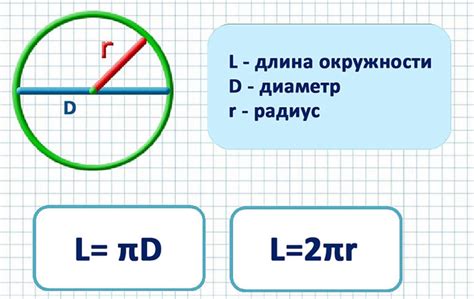
Формула для расчета длины окружности шара:
Длина окружности = 2πr
где:
π (пи) - математическая константа, которая примерно равна 3,14159
r - радиус шара
Таким образом, чтобы найти длину окружности шара, необходимо умножить радиус на два и на число π.
Например, если радиус шара равен 5 см, то формула будет выглядеть так:
Длина окружности = 2 * 3,14159 * 5 = 31,4159 см
Эта формула проста в использовании и позволяет быстро вычислить длину окружности шара, имея только информацию о его радиусе.
Зная длину окружности шара, можно решать различные задачи, связанные с геометрией и механикой, а также использовать эту информацию при расчете объема и площади поверхности шара.
Использование радиуса для расчета окружности шара
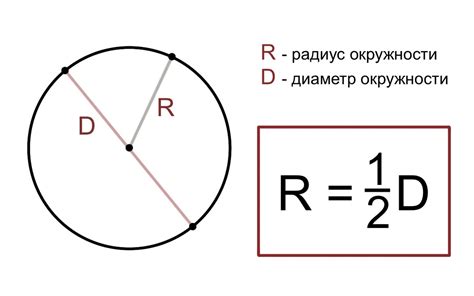
Формула для расчета длины окружности шара используя радиус выглядит следующим образом:
Длина окружности = 2πr
где r - радиус шара, π (пи) - математическая константа, примерно равная 3.14159.
Таким образом, чтобы найти длину окружности шара, необходимо умножить радиус на 2π (пи).
Пример расчета:
- Пусть радиус шара r = 5 см
- Длина окружности шара = 2π * 5 = примерно 31.4159 см
Использование радиуса для расчета окружности шара является простым и удобным способом получить нужные значения без необходимости измерения самой окружности.
Сумма длин окружностей шаров различного радиуса
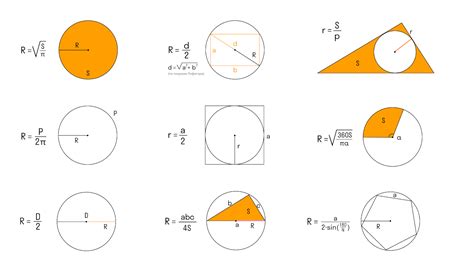
Сумма длин окружностей шаров различного радиуса зависит от самих радиусов и количества шаров. Для расчета этой суммы можно использовать простую формулу, если известны значения радиусов каждого шара.
Формула для расчета длины окружности:
Длина окружности = 2 * π * Радиус
Для получения суммы длин окружностей необходимо сложить длины окружностей каждого шара. При этом нужно учитывать, что каждый шар имеет свой радиус.
Пример расчета суммы длин окружностей двух шаров с разными радиусами:
- Шар 1: Радиус = 4 см
- Шар 2: Радиус = 6 см
Расчет:
- Длина окружности шара 1 = 2 * π * 4 см = 8 * π см
- Длина окружности шара 2 = 2 * π * 6 см = 12 * π см
Сумма длин окружностей шаров = 8 * π см + 12 * π см = 20 * π см
Таким образом, сумма длин окружностей шаров с радиусами 4 см и 6 см равна 20 * π см.
Данная формула может быть использована для расчета суммы длин окружностей шаров с любыми значениями радиусов.
Приложения и примеры расчета окружности шара в реальной жизни
Расчет окружности шара находит применение в различных сферах, где важны соотношения и свойства сферических объектов. Вот несколько примеров расчета окружности шара в реальной жизни:
- Инженерное строительство: при проектировании куполов и сферических конструкций необходимо знать длину окружности, чтобы правильно расположить элементы и оценить необходимое количество материала.
- Медицина: при проведении операций малых размеров, например, в нейрохирургии, длина окружности шарового инструмента может быть важной характеристикой для успешного проведения процедуры.
- Проектирование спортивных мячей: знание длины окружности шара позволяет проектировать мячи с оптимальными размерами и характеристиками, учитывая требования к игровым свойствам и эргономике использования.
- Архитектура и дизайн: при создании иллюстраций проектов или моделей архитектурных сооружений используются правильные сферические формы, для которых важно знать длину окружности.
- Геодезия и картография: расчет окружности шара применяется для определения общей длины линий на поверхности Земли, что позволяет более точно планировать и строить дороги, линии электропередачи и другие коммуникации.
Это лишь несколько примеров применения расчета окружности шара в реальной жизни. Зная формулу и умея ее применять, можно получить множество других полезных результатов и применений в различных областях.