Длина отрезка – одна из основных характеристик геометрических фигур, широко используемая в математике и физике. Ее расчет позволяет определить протяженность отрезка между двумя заданными точками на плоскости или в пространстве.
Для нахождения длины отрезка по координатам двух точек применяется известная формула, основанная на теореме Пифагора. Согласно этой формуле, длина отрезка равна квадратному корню из суммы квадратов разностей координат в заданных точках.
Для того чтобы проиллюстрировать эту формулу, рассмотрим простой пример. Пусть у нас есть отрезок, заданный координатами A(1, 2) и B(4, 6). Чтобы найти его длину, необходимо вычислить разность значений координат по оси X и оси Y для каждой точки, затем возведенные в квадрат суммируются. В итоге, по получившейся сумме берется квадратный корень:
[расчет]
Как найти длину отрезка по координатам

Для расчета длины отрезка по координатам двух точек необходимо применить формулу расстояния между двумя точками в декартовой системе координат.
Формула расстояния между двумя точками:
d = √((x2 - x1)² + (y2 - y1)²)
где:
- d - длина отрезка
- (x1, y1) - координаты первой точки
- (x2, y2) - координаты второй точки
- √ - квадратный корень
Давайте рассмотрим пример:
У нас есть две точки с координатами (3, 4) и (6, 8).
Применим формулу:
d = √((6 - 3)² + (8 - 4)²)
d = √(3² + 4²)
d = √(9 + 16)
d = √25
d = 5
Таким образом, длина отрезка между точками (3, 4) и (6, 8) равна 5.
Определение длины отрезка на плоскости
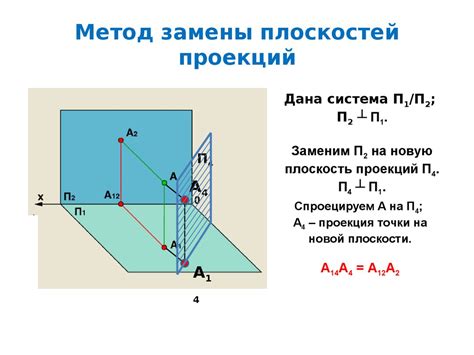
Для определения длины отрезка на плоскости необходимо знать координаты двух его концов. Существует простая формула, позволяющая рассчитать длину отрезка с использованием этих координат.
Пусть A(x1, y1) и B(x2, y2) - координаты концов отрезка. Тогда длина отрезка AB вычисляется по формуле:
AB = √((x2 - x1)² + (y2 - y1)²)
Применение этой формулы позволяет точно определить длину отрезка на плоскости, учитывая его координаты.
Например, пусть A(2, 3) и B(5, 7) - координаты концов отрезка AB. Применяя формулу расчета длины отрезка, получаем:
AB = √((5 - 2)² + (7 - 3)²) = √(3² + 4²) = √(9 + 16) = √25 = 5
Таким образом, длина отрезка AB равна 5 единицам длины.
Формула для расчета длины отрезка

Длина отрезка на плоскости может быть рассчитана с использованием формулы расстояния между двумя точками в двумерной системе координат. Это полезно при работе с геометрическими фигурами или при измерении расстояния между двумя точками.
Формула для расчета длины отрезка между двумя точками (x1, y1) и (x2, y2) на плоскости:
d = √((x2 - x1)² + (y2 - y1)²)
где:
- d - длина отрезка между двумя точками;
- x1, y1 - координаты первой точки;
- x2, y2 - координаты второй точки.
Данная формула представляет собой применение теоремы Пифагора для прямоугольного треугольника, образованного отрезком и осями координат.
Например, для нахождения длины отрезка между точками с координатами (1, 2) и (4, 6), необходимо подставить значения в формулу:
d = √((4 - 1)² + (6 - 2)²) = √((3)² + (4)²)
d = √(9 + 16) = √25 = 5
Таким образом, длина отрезка между точками (1, 2) и (4, 6) равна 5 единицам.
Примеры расчета длины отрезка

Для лучшего понимания формулы расчета длины отрезка по координатам двух точек, рассмотрим несколько примеров.
Пример 1:
Даны две точки:
Точка А: (2, 3)
Точка B: (5, 7)
Для расчета длины отрезка AB, используем формулу:
d = √((x2-x1)² + (y2-y1)²)
Подставив значения координат из примера, получим:
d = √((5-2)² + (7-3)²)
d = √(3² + 4²)
d = √(9 + 16)
d = √25
d = 5
Таким образом, длина отрезка AB равна 5.
Пример 2:
Даны две точки:
Точка А: (0, 0)
Точка B: (8, 15)
Используем формулу расчета длины отрезка:
d = √((x2-x1)² + (y2-y1)²)
Подставим значения координат из примера:
d = √((8-0)² + (15-0)²)
d = √(8² + 15²)
d = √(64 + 225)
d = √289
d = 17
Таким образом, длина отрезка AB равна 17.
Пример 3:
Даны две точки:
Точка А: (-3, -2)
Точка B: (4, 6)
Используем формулу расчета длины отрезка:
d = √((x2-x1)² + (y2-y1)²)
Подставим значения координат из примера:
d = √((4-(-3))² + (6-(-2))²)
d = √((4+3)² + (6+2)²)
d = √(7² + 8²)
d = √(49 + 64)
d = √113
Таким образом, длина отрезка AB равна √113.
Как найти длину отрезка в трехмерном пространстве
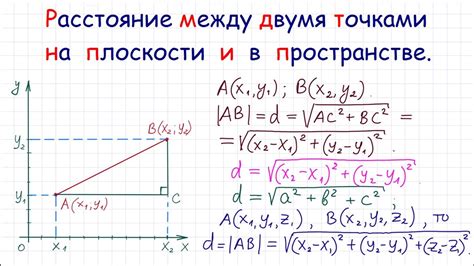
В трехмерном пространстве длина отрезка вычисляется по формуле расстояния между двумя точками. Давайте рассмотрим шаги, необходимые для нахождения этой длины.
1. Запишите координаты двух точек, между которыми вы хотите вычислить длину отрезка. Пусть первая точка имеет координаты (x1, y1, z1), а вторая точка - (x2, y2, z2).
2. Вычислите разность координат по каждой оси, чтобы найти расстояние между точками. В трехмерном пространстве формула для этого выглядит следующим образом:
dx = x2 - x1 dy = y2 - y1 dz = z2 - z13. Возведите разности координат в квадрат:
dx2 = dx * dx dy2 = dy * dy dz2 = dz * dz4. Примените теорему Пифагора к полученным значениям, чтобы найти квадрат длины отрезка:
d2 = dx2 + dy2 + dz25. Наконец, вычислите фактическую длину отрезка, извлекая квадратный корень из полученного значения:
d = sqrt(d2)Таким образом, длина отрезка в трехмерном пространстве равна d.
Давайте рассмотрим пример. Пусть первая точка имеет координаты (1, 2, 3), а вторая точка - (4, 5, 6). Вычислим длину отрезка.
Разность координат:
dx = 4 - 1 = 3 dy = 5 - 2 = 3 dz = 6 - 3 = 3Квадрат разности координат:
dx2 = 3 * 3 = 9 dy2 = 3 * 3 = 9 dz2 = 3 * 3 = 9Квадрат длины отрезка:
d2 = 9 + 9 + 9 = 27Длина отрезка:
d = sqrt(27) ≈ 5.196Таким образом, длина отрезка между точками (1, 2, 3) и (4, 5, 6) составляет около 5.196 единицы длины.
Формула для расчета длины отрезка в трехмерном пространстве

Формула для расчета длины отрезка между двумя точками A(x1, y1, z1) и B(x2, y2, z2) в трехмерном пространстве:
d = √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)
где d - длина отрезка между точками A и B.
Пример расчета длины отрезка для точек A(1, 2, 3) и B(4, 5, 6):
- Вычисляем разности координат для каждой оси:
- (x2 - x1) = (4 - 1) = 3
- (y2 - y1) = (5 - 2) = 3
- (z2 - z1) = (6 - 3) = 3
- Возводим каждую разность в квадрат:
- (x2 - x1)^2 = 3^2 = 9
- (y2 - y1)^2 = 3^2 = 9
- (z2 - z1)^2 = 3^2 = 9
- Суммируем квадраты разностей координат:
- 9 + 9 + 9 = 27
- Находим квадратный корень от суммы:
- √27 ≈ 5.196
Таким образом, длина отрезка между точками A(1, 2, 3) и B(4, 5, 6) в трехмерном пространстве равна примерно 5.196.
Примеры расчета длины отрезка в трехмерном пространстве
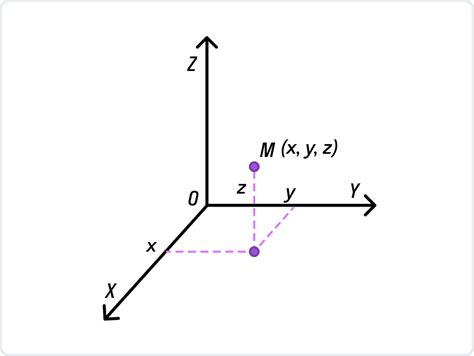
Для расчета длины отрезка в трехмерном пространстве необходимо знать координаты начальной точки A(x1, y1, z1) и конечной точки B(x2, y2, z2). Будем использовать формулу:
| Пример | Координаты начальной точки A | Координаты конечной точки B | Расчет длины AB |
|---|---|---|---|
| Пример 1 | A(1, 2, 3) | B(4, 5, 6) | |
| Пример 2 | A(0, 0, 0) | B(0, 0, 5) | |
| Пример 3 | A(2, -3, 1) | B(-4, 0, 5) |
В данных примерах показан расчет длины отрезка AB в трехмерном пространстве с использованием формулы. Результат вычисляется как квадратный корень суммы квадратов разностей координат. Длина отрезка AB в каждом примере представлена в соответствующем столбце таблицы.