Трапеция – фигура, имеющая две параллельные стороны и две непараллельные стороны. Одной из важных характеристик трапеции является её средняя линия. Нахождение длины этого отрезка может быть полезным при решении различных задач, связанных с геометрией. В данной статье мы рассмотрим формулы и способы определения длины средней линии трапеции.
Средняя линия трапеции это отрезок, соединяющий середины её непараллельных сторон. Для его нахождения необходимо знать длины этих сторон или другие параметры трапеции, такие как высоту или углы. Однако, есть несколько универсальных формул, позволяющих вычислить длину средней линии при различных условиях.
Если известны только длины оснований трапеции, то можно воспользоваться формулой:
Медиана = (сумма длин оснований) / 2
Если известны длины оснований и высота трапеции, то формула будет следующей:
Медиана = (длина большего основания + длина меньшего основания) / 2
Для трапеции с известными углами a и b, и зная длину одного из оснований, можно найти длину средней линии по формуле:
Медиана = √(основание² + d²), где d – расстояние между серединами непараллельных сторон.
Таким образом, существует несколько способов определения длины средней линии трапеции в зависимости от того, какие параметры трапеции известны. Используя соответствующие формулы, можно решать задачи, связанные с этой геометрической фигурой.
Способы определения длины отрезка средней линии трапеции
1. Использование формулы
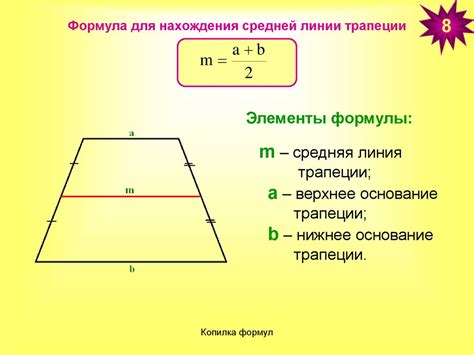
Для нахождения длины отрезка средней линии трапеции можно использовать специальную формулу. Для обозначения длины отрезка часто используется символ м. Формула для нахождения длины отрезка средней линии трапеции выглядит следующим образом:
м = (а + b) / 2,
где а и b – длины параллельных сторон трапеции.
2. Использование диагонали
Другим способом определения длины отрезка средней линии трапеции является использование длины диагонали. Для этого нужно знать длины боковых сторон трапеции и длину одной из диагоналей. Зная эти данные, можно воспользоваться формулой:
м = √(a2 – c2),
где а – длина одной из диагоналей трапеции, с – половина разности длин параллельных сторон.
3. Использование площади
Третий способ нахождения длины отрезка средней линии трапеции основан на использовании площади фигуры. Если известны длины всех сторон трапеции и ее площадь, то длина отрезка может быть вычислена с помощью следующей формулы:
м = 2S / (a + b),
где S – площадь трапеции, а и b – длины параллельных сторон.
Формула для расчета длины отрезка средней линии трапеции
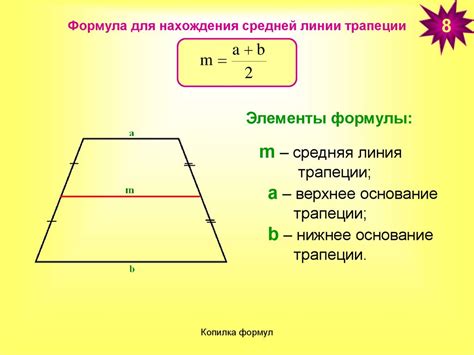
Длина отрезка средней линии трапеции может быть рассчитана с помощью следующей формулы:
lср = (a + b) / 2
где lср - длина отрезка средней линии трапеции,
a - длина одного основания трапеции,
b - длина другого основания трапеции.
Формула основана на принципе среднего значения оснований трапеции. Чтобы найти длину отрезка средней линии трапеции, необходимо сложить длины обоих оснований и разделить полученную сумму на 2.
Например, если длина одного основания трапеции равна 6 см, а длина другого - 8 см, то длина отрезка средней линии будет равна:
lср = (6 + 8) / 2 = 14 / 2 = 7 см
Таким образом, длина отрезка средней линии трапеции в данном случае равна 7 см.
Геометрический метод вычисления длины отрезка средней линии трапеции
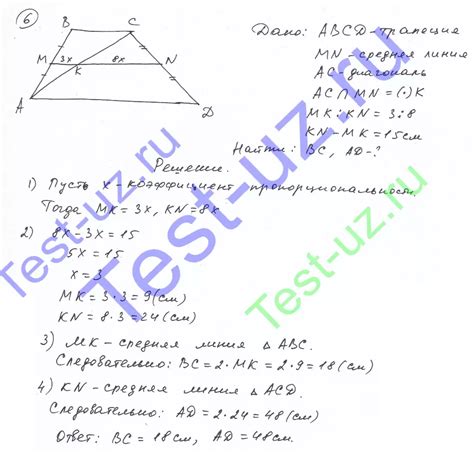
Для применения геометрического метода вычисления длины отрезка средней линии трапеции необходимо знать длины оснований трапеции (a и b) и расстояние между ними (h).
Шаги для вычисления длины средней линии трапеции:
- Найдите разность длин оснований трапеции: b - a.
- Умножьте полученную разность на половину высоты трапеции: 0.5 * h.
- Сложите полученное произведение с меньшим основанием (a).
Формула для вычисления длины отрезка средней линии трапеции выглядит следующим образом:
Длина средней линии = a + 0.5 * (b - a)
Геометрический метод вычисления длины отрезка средней линии трапеции позволяет получить точный результат при известных значениях оснований и высоты трапеции. Этот метод широко применяется в геометрии и строительстве для вычисления различных характеристик фигур.