Равнобедренный треугольник – это треугольник, у которого две стороны равны. Так как углы при основании равнобедренного треугольника также равны, то его основание – это отрезок, соединяющий две неравные стороны.
Если известны длина сторон равнобедренного треугольника и требуется найти длину отрезка, соединяющего середины его неравных сторон, применяется простая формула. Для этого достаточно знать значение основания треугольника и использовать величину этого отрезка, равную половине длины основания.
Представим, что длина основания равнобедренного треугольника составляет a, а длина отрезка между серединами неравных сторон равна b. Используя простую формулу, мы можем выразить длину отрезка:
b = a/2
Таким образом, для расчета значения отрезка в равнобедренном треугольнике достаточно разделить длину основания на 2.
Давайте рассмотрим пример: у нас есть равнобедренный треугольник, у которого длина основания составляет 10 сантиметров. Чтобы найти длину отрезка между серединами неравных сторон, мы применим простую формулу:
b = 10/2 = 5
Таким образом, длина отрезка равна 5 сантиметрам.
Что такое равнобедренный треугольник
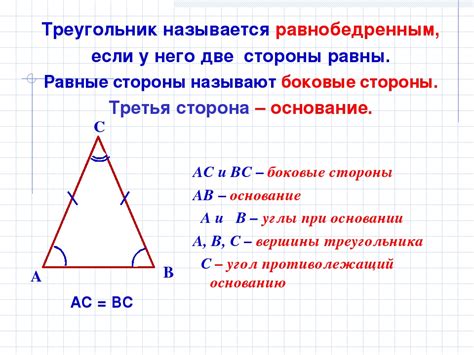
В равнобедренном треугольнике две равные стороны называются бедрами, а третья сторона - основанием.
Уравнение равнобедренного треугольника можно записать следующим образом: AB = AC, где AB и AC - бедра треугольника, а BC - основание.
Равнобедренные треугольники имеют ряд особенностей и свойств. Например, углы при основании равнобедренного треугольника также равны между собой, а высота проведенная к основанию является биссектрисой угла при основании.
Формула для вычисления длины отрезка в равнобедренном треугольнике
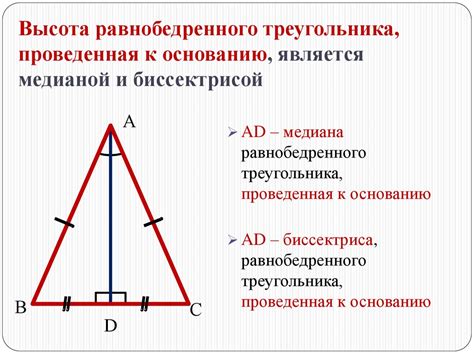
В равнобедренном треугольнике, два из трех его сторон равны. Это значит, что для нахождения длины отрезка в таком треугольнике можно использовать простую формулу.
Формула для вычисления длины отрезка в равнобедренном треугольнике:
AB = AC = BC = d, где d - длина отрезка.
То есть, все стороны треугольника равны между собой.
Примеры:
1. Рассмотрим равнобедренный треугольник ABC, где длина отрезка AB равна 5 см. Так как треугольник равнобедренный, то AB = AC = BC. Следовательно, длина отрезка AC и BC также равна 5 см.
2. Пусть у нас есть равнобедренный треугольник XYZ. Известно, что длина отрезка XY равна 8 метров. Так как треугольник равнобедренный, то XY = XZ = YZ. Значит, длина отрезка XZ и YZ также равна 8 метров.
Простая формула для вычисления отрезка в равнобедренном треугольнике
Для нахождения длины отрезка в равнобедренном треугольнике используется простая и удобная формула. В равнобедренном треугольнике у двух сторон равны длины. Это означает, что если известна длина основания и высота, можно легко вычислить длину боковой стороны.
Формула для вычисления длины отрезка в равнобедренном треугольнике выглядит следующим образом:
Длина отрезка = 2 * (длина основания / 2) * (высота / длина основания)
Рассмотрим пример:
Пусть у равнобедренного треугольника длина основания равна 8 см, а высота равна 6 см. Применяя формулу, получаем:
Длина отрезка = 2 * (8 / 2) * (6 / 8) = 2 * 4 * 0.75 = 6 см
Таким образом, длина отрезка в данном треугольнике составляет 6 см.
Используя данную простую формулу, можно легко находить длину отрезка в равнобедренных треугольниках, имея информацию о длине основания и высоте.
Примеры вычисления длины отрезка в равнобедренном треугольнике
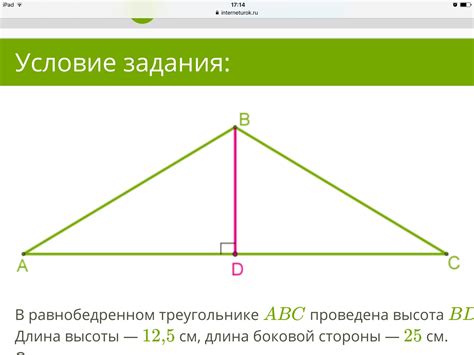
Для вычисления длины отрезка в равнобедренном треугольнике можно использовать следующую формулу:
Длина отрезка AB = AC = BC, где AC и BC - боковые стороны треугольника, а AB - основание. Это свойство равнобедренного треугольника позволяет нам сразу же найти длину отрезка, зная длину боковых сторон.
Ниже приведены примеры вычисления длины отрезка в равнобедренном треугольнике:
Пример 1:
В равнобедренном треугольнике ABC известна длина основания AB, которая составляет 6 единиц длины. Необходимо найти длину боковой стороны AC.
Решение:
Поскольку треугольник ABC является равнобедренным, то AC = AB = BC. Значит, длина боковой стороны AC равна 6 единиц длины.
Ответ: длина боковой стороны AC равна 6 единиц длины.
Пример 2:
В равнобедренном треугольнике XYZ известна длина боковой стороны XY, которая составляет 8 единиц длины. Необходимо найти длину основания ZY.
Решение:
Поскольку треугольник XYZ является равнобедренным, то XY = ZY. Значит, длина основания ZY равна 8 единиц длины.
Ответ: длина основания ZY равна 8 единиц длины.
Как применить формулу для вычисления отрезка в равнобедренном треугольнике
Для вычисления длины отрезка в равнобедренном треугольнике можно использовать простую формулу, которая основана на свойствах равнобедренности.
Пусть у нас есть равнобедренный треугольник ABC, в котором стороны AB и AC равны между собой. Нам нужно найти длину отрезка DE, который является высотой треугольника и проходит через вершину A.
Формула, которая позволяет вычислить длину отрезка DE, выглядит следующим образом:
DE = √(AD * DB)
Здесь AD - половина длины стороны AB, а DB - половина длины стороны AC. Чтобы найти AD и DB, можно воспользоваться свойством равенства сторон треугольника.
Рассмотрим пример:
У нас есть равнобедренный треугольник ABC, в котором стороны AB и AC равны 6 единиц. Нам нужно найти длину отрезка DE.
Сначала найдем AD и DB. Поскольку треугольник равнобедренный, стороны AB и AC равны между собой. Таким образом, AD = DB = 6 / 2 = 3.
Теперь, используя формулу, мы можем найти длину отрезка DE:
DE = √(3 * 3) = √9 = 3
Таким образом, длина отрезка DE в нашем равнобедренном треугольнике равна 3 единицам.
Эта формула может быть полезна при решении различных задач, связанных с равнобедренными треугольниками. Она позволяет легко и быстро вычислить длину отрезка, проходящего через вершину треугольника и перпендикулярного к основанию.