Треугольник - это одна из основных геометрических фигур, состоящая из трех сторон и трех углов. В геометрии существует множество способов вычисления сторон и углов треугольников, включая известные три стороны или две стороны и внутренний угол.
Однако, иногда у нас может быть известна только одна сторона треугольника и тангенс угла, и мы хотим найти другую сторону. Но не отчаивайтесь! В данной статье мы расскажем вам подробные инструкции и приведем несколько примеров, чтобы помочь вам разобраться с этой задачей.
Для решения этой задачи мы воспользуемся теоремой тангенсов. Вспомните, что тангенс угла - это отношение противоположной стороны к прилежащей стороне. То есть, если у нас есть известная сторона треугольника и тангенс угла, мы можем использовать его для нахождения противоположной стороны.
Теперь давайте рассмотрим подробный пример. Предположим, у нас есть треугольник ABC, где известна сторона AB и тангенс угла C. Мы хотим найти сторону BC.
Как найти сторону треугольника
Если вам дано значение тангенса угла и известная длина одной из сторон треугольника, вы можете найти длину другой стороны при помощи простых математических вычислений:
- Определите значение синуса угла, для которого дано значение тангенса. Вы можете использовать таблицу синусов или калькулятор с тригонометрическими функциями.
- Используя значение синуса и известную сторону треугольника, вычислите противолежащую сторону по формуле противолежащая сторона = известная сторона * синус угла.
Например, если дано значение тангенса угла равное 0.5 и известная сторона равна 10 единицам, найдем противолежащую сторону:
Значение синуса для угла, у которого тангенс равен 0.5, равно 0.4755 (с точностью до четырех знаков после запятой).
Противолежащая сторона = 10 * 0.4755 = 4.755 единиц.
Таким образом, значение противолежащей стороны треугольника равно 4.755 единицам.
С тангенсом угла и известной стороной
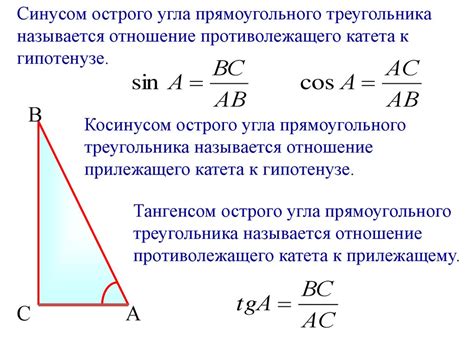
Если вам дан треугольник, в котором известны значение тангенса одного из углов и длина одной из сторон, вы можете найти длину другой стороны треугольника с помощью тригонометрических функций. Для этого вам понадобится знание геометрии и умение работать с углами и сторонами треугольника.
Для начала определите угол, тангенс которого известен, и сторону, длина которой вам дана. Обозначим угол как α и длину стороны как a.
Затем используйте тригонометрическое соотношение вида:
тангенс(α) = противолежащая сторона / прилежащая сторона
Если вам известен тангенс угла α и длина стороны a, то вы можете выразить противолежащую сторону как:
противолежащая сторона = тангенс(α) * прилежащая сторона
Наконец, подставьте значения тангенса угла и длины известной стороны в формулу и рассчитайте длину противолежащей стороны.
Приведем пример для наглядности. Предположим, что у нас есть треугольник ABC, угол A равен 30°, длина стороны AB равна 4 единицы. Мы хотим найти длину стороны AC.
Используя тригонометрию, мы можем найти тангенс угла A:
тангенс(30°) = противолежащая сторона / прилежащая сторона
тангенс(30°) = AC / AB
Затем мы можем переписать формулу, чтобы найти длину противолежащей стороны:
AC = тангенс(30°) * AB
Подставляя известные значения, получим:
AC = тангенс(30°) * 4
Рассчитывая это выражение, мы найдем, что длина стороны AC равна примерно 2,31 единицы.
Теперь у вас есть общее представление о том, как найти сторону треугольника с известным тангенсом угла и известной стороной. Важно запомнить соответствующие формулы и выполнять необходимые математические вычисления.
Определение тангенса угла

Тангенс угла обычно обозначается как tg или tan.
Для вычисления тангенса угла необходимо знать длину противолежащей стороны и длину прилежащей стороны треугольника. Тангенс угла может быть вычислен с использованием тригонометрических таблиц или калькулятора с функцией тангенса.
| Теорема | Вычисление тангенса угла |
|---|---|
| Теорема тангенса | Если известны длина противолежащей стороны (a) и длина прилежащей стороны (b) треугольника, то тангенс угла (α) может быть вычислен по формуле: tg(α) = a / b. |
| Использование тригонометрических таблиц | Тангенс угла может быть найден, используя значения из тригонометрической таблицы для соответствующего угла. |
| Использование калькулятора с функцией тангенса | Современные калькуляторы обычно имеют встроенную функцию тангенса, которая позволяет вычислить значение тангенса угла по введенным данным. |
Знание тангенса угла может быть полезным при решении различных задач, связанных с геометрией, физикой и инженерией.
Формула для нахождения стороны
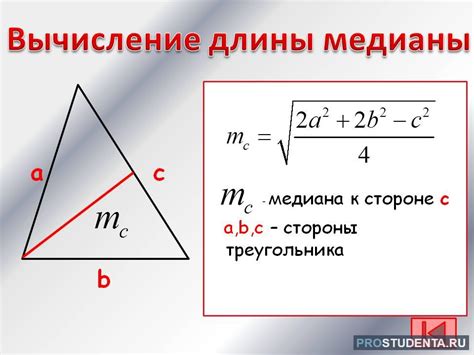
При нахождении стороны треугольника с тангенсом угла и известной стороной можно использовать формулу:
Сторона = известная сторона / тангенс угла
Для использования данной формулы необходимо знать значение известной стороны и тангенса угла, который требуется найти. Тангенс угла можно найти, используя соотношение:
тангенс угла = противолежащая сторона / прилежащая сторона
После нахождения значения тангенса угла, можно подставить его в формулу и вычислить значение искомой стороны. Например, если известна сторона треугольника равная 5 см, а тангенс угла равен 1, то:
Сторона = 5 см / 1 = 5 см
Таким образом, сторона треугольника будет равна 5 см.
Шаги для решения задачи
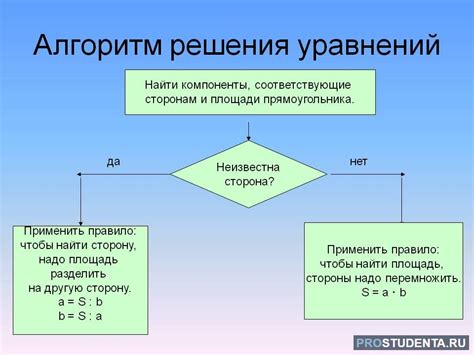
Для решения задачи о нахождении стороны треугольника с тангенсом угла и известной стороной следуйте этим шагам:
Шаг 1: Известная сторона треугольника обозначается как a, а тангенс угла - как tan(α), где α - угол треугольника.
Шаг 2: Раскройте определение тангенса угла. Тангенс угла равен отношению противолежащей стороны к прилежащей стороне: tan(α) = a / x, где x - неизвестная сторона треугольника.
Шаг 3: Исключите неизвестное значение из уравнения, перемещая переменные. Умножьте обе части уравнения на x: x * tan(α) = a.
Шаг 4: Разделите обе части уравнения на tan(α): x = a / tan(α). Полученное значение x будет стороной треугольника, которую необходимо найти.
Теперь у вас есть алгоритмический набор шагов для решения задачи о нахождении стороны треугольника с тангенсом угла и известной стороной. Просто подставьте значения в формулу и выполните вычисления, чтобы получить искомую сторону треугольника.
Пример 1: Нахождение стороны треугольника
Предположим, у нас есть треугольник ABC, в котором известна одна из сторон, а также значение тангенса угла между этой стороной и другой стороной треугольника (катетом).
Для начала обозначим известные значения:
Сторона AB равна a.
Тангенс угла A равен tg(A) = k.
Теперь можем воспользоваться определением тангенса:
tg(A) = k = синус угла A / косинус угла A.
Так как тангенс угла A известен, аналогично для синуса и косинуса:
k = sin(A) / cos(A).
Используя формулу синуса и косинуса:
a / AB = sin(A) / cos(A).
Преобразуем полученное равенство:
a = AB * (sin(A)/cos(A)).
Таким образом, сторона треугольника AB равна a = AB * (sin(A)/cos(A)).
Для нахождения значения стороны треугольника AB, нужно знать значение синуса и косинуса угла A. Можно воспользоваться таблицами значений синуса и косинуса углов или использовать калькулятор с тригонометрическими функциями.
Пример:
Пусть значения стороны AB равно 5 и тангенс угла A равен 0.75. Найдем сторону треугольника AB.
a = 5 * (sin(A)/cos(A)).
Так как tg(A) = k = 0.75, то можем выразить sin(A) и cos(A):
sin(A) = k * cos(A).
Теперь можем подставить значения sin(A) и cos(A) в формулу для нахождения стороны треугольника:
a = 5 * (0.75 * cos(A) / cos(A)) = 5 * 0.75 = 3.75.
Таким образом, сторона треугольника AB равна 3.75.
Пример 2: Проверка результата
После расчета стороны треугольника с использованием тангенса угла и известной стороны, важно проверить полученный результат. Возьмем, например, треугольник ABC, где сторона AB равна 6 см, а угол BAC имеет тангенс 0,5.
Сначала мы используем формулу для расчета стороны BC:
BC = AB * tan(BAC)
BC = 6 * 0,5
BC = 3
После получения значения 3 см, мы можем проверить результат, используя другие известные параметры треугольника.
Например, мы можем воспользоваться теоремой Пифагора для проверки значения стороны BC:
AC^2 = AB^2 + BC^2
AC^2 = 6^2 + 3^2
AC^2 = 36 + 9
AC^2 = 45
Сравнивая полученное значение AC^2 суммы квадратов сторон AB и BC со значением 45, мы убеждаемся, что результат расчета стороны BC равен 3 см верен.
Таким образом, мы успешно нашли сторону треугольника с использованием тангенса угла и известной стороны, а также проверили правильность полученного результата.