Геометрия – одна из важных разделов математики, который изучает формы, размеры и свойства геометрических фигур. Один из интересных объектов в геометрии – треугольник.
Внутри треугольника можно вписать окружность, такую окружность называют вписанной. Интересный факт состоит в том, что если мы знаем радиус вписанной окружности и длину одной из сторон треугольника, то с помощью формулы, будем называть ее формулой Герона, можно найти длину двух оставшихся сторон. Применение данной формулы может быть полезным при решении различных геометрических задач.
В данной статье мы рассмотрим, как найти длину стороны треугольника, если известен радиус вписанной окружности. Также рассмотрим понятие циклического треугольника и приведем примеры для наглядности.
Как определить длину стороны треугольника с радиусом вписанной окружности?

В геометрии существует способ определения длины стороны треугольника, если известен радиус вписанной окружности. Для этого можно использовать формулу, основанную на теореме о радиусе окружности, вписанной в треугольник:
Формула: Длина стороны треугольника равна произведению радиуса вписанной окружности на синус половины угла, образованного этой стороной.
Предположим, у нас есть треугольник ABC, в котором радиус вписанной окружности равен r. Для вычисления длины стороны AB, мы должны знать значение угла A, образованного этой стороной.
Применим формулу:
Длина AB = 2 * r * sin(A/2)
Где sin(A/2) - синус половины угла A, который можно вычислить по таблице значений синусов или с помощью калькулятора.
Таким образом, используя данную формулу, мы можем определить длину стороны треугольника с радиусом вписанной окружности, если известно значение радиуса и соответствующего угла треугольника.
Определение радиуса вписанной окружности треугольника
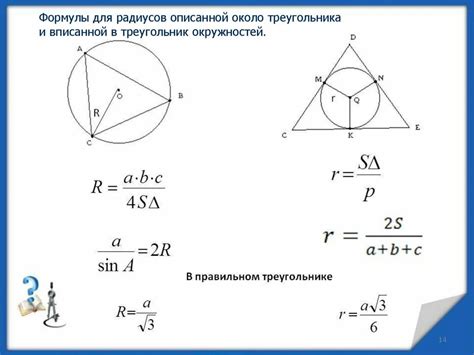
Для определения радиуса вписанной окружности треугольника существует несколько формул, в зависимости от доступных данных. Одним из способов вычисления радиуса является использование формулы:
| r = S / p |
где S - площадь треугольника, а p - полупериметр (половина суммы длин всех сторон).
Другой способ вычисления радиуса вписанной окружности треугольника связан с использованием длин сторон треугольника. Он основан на формуле Герона для вычисления площади треугольника:
| p = (a + b + c) / 2 |
| S = sqrt(p * (p - a) * (p - b) * (p - c)) |
где a, b и c - длины сторон треугольника, а sqrt - квадратный корень.
Получив значение площади S, можно использовать первую формулу для определения радиуса вписанной окружности.
Определение радиуса вписанной окружности треугольника позволяет расширить наши знания о геометрических свойствах этой фигуры и применять их в различных математических задачах.
Формулы для расчета длины стороны треугольника

Для начала необходимо вспомнить основные понятия связанные с вписанной окружностью. Радиус вписанной окружности - это отрезок, проведенный из центра окружности до одной из ее точек касания с стороной треугольника. Так же есть вспомогательная линия, проведенная из центра окружности до точки пересечения сторон треугольника.
Формула для вычисления длины стороны треугольника с радиусом вписанной окружности выглядит следующим образом:
- Дано:
- Радиус вписанной окружности (r)
- Длина стороны треугольника (a) = 2 * r * tan(π/3)
Для применения данной формулы необходимо знать радиус вписанной окружности. Подставляя значение радиуса в формулу, можно вычислить длину стороны треугольника.
Пример:
- Дано:
- Радиус вписанной окружности (r) = 5 см
- Длина стороны треугольника (a) = 2 * 5 * tan(π/3)
- Длина стороны треугольника (a) ≈ 10 * 1.732 ≈ 17.32 см
Таким образом, длина стороны треугольника, с радиусом вписанной окружности равным 5 см, составляет примерно 17.32 см.
Циклический треугольник в геометрии

В циклическом треугольнике существует ряд интересных свойств:
- Сумма всех углов в циклическом треугольнике равна 180 градусам.
- Противоположные углы циклического треугольника суммируются до 180 градусов.
- Сумма двух углов, образованных стороной треугольника и хордой, является постоянной величиной и равна обратному углу, под которым хорда видна из центра окружности.
- Площадь циклического треугольника можно найти по формуле: S = (R^2 * sin(A) * sin(B) * sin(C)) / 4, где R - радиус вписанной окружности, А, В и С - углы треугольника.
Для решения задачи о нахождении длины стороны треугольника с заданным радиусом вписанной окружности, можно использовать теорему синусов или косинусов. Эти теоремы позволяют найти длины сторон треугольника, если известны значения радиуса R и одного угла треугольника.
Таким образом, циклический треугольник является одним из интересных объектов в геометрии, который имеет ряд уникальных свойств и может быть использован для решения различных задач в данной области.
Определение циклического треугольника
Зная радиус вписанной окружности, можно определить длину стороны циклического треугольника. Для этого существует формула, связывающая радиус вписанной окружности и длины сторон треугольника.
Формула для определения длины стороны циклического треугольника:
a = 2R*sin(A)
где:
- a - длина стороны треугольника;
- R - радиус вписанной окружности;
- A - угол между сторонами треугольника, направленными от вершины к противолежащим сторонам.
Эта формула позволяет вычислить длину каждой из сторон циклического треугольника. Зная длины сторон, можно также построить и другие соотношения и свойства треугольника, такие как площадь и высоты.
Примеры циклических треугольников
- Равносторонний треугольник является циклическим, так как вокруг вписанной окружности можно описать сам треугольник.
- Прямоугольный треугольник с углом 90 градусов также может быть циклическим треугольником, если гипотенуза служит диаметром окружности, а прямые углы лежат на окружности.
- Остроугольный треугольник может быть циклическим, если точка пересечения высот, описанная окружность и стороны треугольника лежат на одной окружности.
Приведенные примеры циклических треугольников являются только небольшой частью разнообразия, которое можно встретить в геометрии. В зависимости от особенностей и условий каждого треугольника, можно определить, является ли он циклическим или нет.