Прямоугольный треугольник - одна из самых известных и простых фигур в геометрии. Он обладает особенностью: две его стороны перпендикулярны друг другу. Это значит, что у прямоугольного треугольника есть особый тип сторон - катеты.
Катеты прямоугольного треугольника - это две из его сторон, образующие прямой угол друг с другом. Всего в таком треугольнике всегда три стороны: два катета и гипотенуза, которая является наибольшей стороной. Важно помнить, что для нахождения второго катета нужно знать длину одного из катетов и гипотенузы.
Существует несколько способов найти второй катет прямоугольного треугольника. Один из них - применение теоремы Пифагора. Согласно этой теореме, сумма квадратов длин катетов равна квадрату длины гипотенузы. Используя эту формулу и известные значения длины одного катета и гипотенузы, можно найти длину второго катета.
Определение условия
При рассмотрении прямоугольного треугольника, второй катет которого неизвестен, мы знаем следующие параметры:
- Длина первого катета (a)
- Длина гипотенузы (c)
Наша задача состоит в определении длины второго катета (b).
Для этого мы можем использовать условие, которое связывает длины сторон прямоугольного треугольника:
a^2 + b^2 = c^2
Где:
- a - длина первого катета
- b - длина второго катета
- c - длина гипотенузы
Используя данное условие, мы можем решить уравнение и найти длину второго катета треугольника.
Формула нахождения второго катета
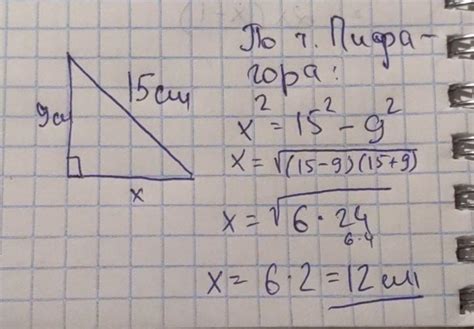
Для нахождения второго катета прямоугольного треугольника можно использовать теорему Пифагора. Согласно этой теореме, сумма квадратов длин катетов равна квадрату гипотенузы.
Итак, пусть a и b - длины катетов, а c - длина гипотенузы прямоугольного треугольника. Тогда формула нахождения второго катета будет выглядеть следующим образом:
a^2 + b^2 = c^2
Для нахождения второго катета необходимо знать длины другого катета и гипотенузы. Подставив известные значения, можно решить полученное уравнение и найти второй катет.
Пример:
Пусть известны длина одного катета a = 3 и длина гипотенузы c = 5. Чтобы найти длину второго катета b, подставим известные значения в формулу:
3^2 + b^2 = 5^2
9 + b^2 = 25
b^2 = 16
b = 4
Таким образом, длина второго катета равна 4.
Примеры решения

Для нахождения второго катета прямоугольного треугольника можно использовать теорему Пифагора или тангенс угла.
Пример 1: Использование теоремы Пифагора
Пусть у нас прямоугольный треугольник со сторонами a = 3 и c = 5. Необходимо найти второй катет b.
Из теоремы Пифагора: c^2 = a^2 + b^2.
Подставляем известные значения: 5^2 = 3^2 + b^2.
Вычисляем: 25 = 9 + b^2.
Вычитаем 9: 16 = b^2.
Извлекаем квадратный корень: b = 4.
Таким образом, второй катет равен 4.
Пример 2: Использование тангенса угла
Пусть у нас прямоугольный треугольник, где угол α = 30°, а гипотенуза c = 6. Необходимо найти второй катет b.
Используя тангенс угла: tan(α) = b / a, где a - прилежащий катет.
Подставляем известные значения: tan(30°) = b / a.
Вычисляем: 0,577 = b / a.
Умножаем обе части уравнения на а: 0,577 * a = b.
Подставляем значение гипотенузы c = 6 и находим a: 0,577 * a = 6.
Решаем уравнение: a = 6 / 0,577 ≈ 10,39.
Таким образом, второй катет примерно равен 10,39.
Практическое применение

Поиск второго катета прямоугольного треугольника может быть полезным для решения множества реальных задач. Например, он может использоваться в архитектуре при планировании строительства, в инженерии при проектировании механизмов, в навигации для определения расстояния и направления движения, а также в медицине для измерения размеров и форм органов.
Кроме того, знание способов нахождения второго катета позволяет эффективно решать задачи в повседневной жизни. Например, при покупке новой мебели или подборе размеров комнаты для ремонта, вы сможете самостоятельно измерить второй катет и убедиться, что предмет или комната подходят вам по размерам.
Знание и умение применять математические знания являются важными навыками для успешной жизни и работы в современном мире. Они помогут вам анализировать и решать сложные задачи, обучаться новым навыкам и находить креативные подходы к различным ситуациям. Поэтому изучение геометрии, включая нахождение второго катета прямоугольного треугольника, является всегда полезным и актуальным.