В математике дроби являются неотъемлемой частью числовой системы. Они позволяют представлять числа, которые не могут быть выражены целыми числами. Однако, в некоторых случаях может возникнуть необходимость найти долю числа при делении на дробь.
Чтобы найти долю числа при делении на дробь, необходимо умножить это число на обратную дробь. Обратная дробь получается путем перестановки числителя и знаменателя дроби.
Допустим, у нас есть число 5 и дробь 1/4. Чтобы найти долю числа 5 при делении на дробь 1/4, необходимо умножить 5 на обратную дробь 4/1. Результатом будет число 20. Это можно записать в виде уравнения:
5 / (1/4) = 5 * (4/1) = 20.
Таким образом, чтобы найти долю числа при делении на дробь, нужно умножить это число на обратную дробь.
Что такое доля числа?

Доля числа показывает, какую долю от общего значения числа занимает конкретное значение. Например, если число 5 разделено на 2 долей, каждая доля будет составлять 2/5 или 0.4 от общего значения. Таким образом, доля числа может быть представлена как десятичная или обыкновенная дробь в диапазоне от 0 до 1.
Вычисление доли числа требует деления числа на соответствующую дробь. Если число делится на дробь, то результат будет показывать отношение доли к общему значению числа. Например, если число 10 делится на 5, то доля числа будет составлять 2, так как 2 * 5 = 10.
Доля числа является важным математическим понятием и используется в различных областях, включая экономику, физику и вероятность. Понимание доли числа позволяет оценивать и анализировать относительные значения и части, что является необходимым во многих практических задачах.
Как найти долю числа при делении на дробь?

Для нахождения доли числа при делении на дробь необходимо выполнить следующие шаги:
- Преобразовать дробь к десятичному виду, если она задана в виде обыкновенной дроби.
- Выполнить деление числа на полученное десятичное значение дроби.
- Умножить полученный результат на 100 для получения доли в процентах, если это требуется.
Например, при делении числа 8 на дробь 1/4, сначала преобразуем дробь 1/4 в десятичную дробь, получая 0.25. Затем выполняем деление числа 8 на 0.25, что равно 32. Итак, доля числа 8 при делении на дробь 1/4 равна 32. Если нам нужно выразить результат в процентах, мы умножаем его на 100 и получаем 3200%.
Таким образом, нахождение доли числа при делении на дробь - это простое математическое действие, которое может быть выполнено путем преобразования дроби к десятичному виду и последующего деления числа на это значение.
Объяснение формулы для нахождения доли числа

При делении числа на дробь, чтобы найти долю числа, необходимо умножить это число на значение, обратное дроби. Формула для нахождения доли числа выглядит следующим образом:
Доля числа = Число / Дробь
Для понимания работы формулы рассмотрим пример. Пусть у нас есть число 10 и дробь 1/2. Чтобы найти долю числа 10, мы должны умножить 10 на значение, обратное дроби 1/2. Значение, обратное дроби 1/2, равно 2. То есть:
| Число | Дробь | Доля числа |
|---|---|---|
| 10 | 1/2 | 10 * 2 = 20 |
Таким образом, доля числа 10 при делении на дробь 1/2 равна 20. Это означает, что 20 является половиной числа 10. Если мы умножим долю числа 20 на дробь 1/2, получим снова число 10, так как 20 * 1/2 = 10.
Теперь, когда мы знаем формулу и принцип работы, мы можем легко находить долю числа при делении на любую дробь. Просто умножаем число на значение, обратное дроби, и получаем искомую долю числа.
Примеры нахождения доли числа
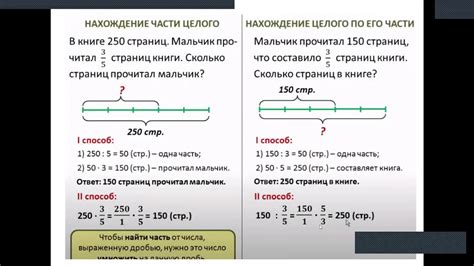
Для того чтобы найти долю числа, необходимо число разделить на дробь, которая представлена в виде числителя и знаменателя. Давайте рассмотрим несколько примеров нахождения доли числа:
Пример 1:
Найти 2/5 числа 50.
Для этого нам нужно разделить 50 на дробь 2/5:
(50 ÷ (2 ÷ 5))
Рассчитаем:
(50 ÷ 2) × 5 = 25 × 5 = 125
Ответ: доля числа 50, равная 2/5, составляет 125.
Пример 2:
Найти 3/8 числа 64.
Разделим 64 на дробь 3/8:
(64 ÷ (3 ÷ 8))
(64 ÷ 3) × 8 = 21.33 × 8 = 170.65
Ответ: доля числа 64, равная 3/8, составляет 170.65.
Пример 3:
Найти 7/10 числа 80.
Разделим 80 на дробь 7/10:
(80 ÷ (7 ÷ 10))
(80 ÷ 7) × 10 = 11.43 × 10 = 114.29
Ответ: доля числа 80, равная 7/10, составляет 114.29.
Таким образом, используя дроби, мы можем находить доли числа и получать результаты в виде десятичных дробей.
Особенности нахождения доли числа при делении на различные дроби

При делении числа на дробь важно учитывать особенности каждого конкретного делителя. Различные дроби могут приводить к различным результам при делении.
Если делитель является простой дробью, то долю числа можно найти, инвертировав делитель и умножив на исходное число. Например, чтобы найти долю числа 5 при делении на 1/2, необходимо умножить 5 на 2/1, что дает результат 10.
Однако, при делении на дробь, равную единице, результат всегда будет исходное число. Например, 5 разделить на 1 даст результат 5.
Если делитель является смешанной дробью, то следует привести ее к неправильной дроби и продолжить вычисления как для простой дроби. Например, для делителя 1 1/2 следует привести его к виду 3/2 и умножить на исходное число.
Также, при делении на дробь, равную нулю, результатом будет бесконечность или неопределенность. Это связано с невозможностью деления на ноль.
Важно помнить, что при нахождении доли числа при делении на дробь, результат будет больше исходного числа, если делитель меньше единицы, и меньше исходного числа, если делитель больше единицы.
Примеры:
- Доля числа 10 при делении на 1/5 равна 10 * 5/1 = 50.
- Доля числа 15 при делении на 2/3 равна 15 * 3/2 = 22.5.
- Доля числа 8 при делении на 1 равна 8.
- Доля числа 20 при делении на 1 1/4 равна 20 * 4/5 = 16.
- При делении на 0 результатом будет бесконечность или неопределенность.
Применение нахождения доли числа в реальной жизни

Нахождение доли числа при делении на дробь имеет множество применений в реальной жизни. Рассмотрим некоторые из них:
- Финансы и бизнес: При расчете процентных ставок, налогов, долей владения компаний и доли дохода или прибыли, нахождение доли числа является неотъемлемой частью финансового анализа и планирования.
- Кулинария: Рецепты и кулинарные пропорции часто требуют нахождения доли числа, чтобы правильно измерить и соотносить количество ингредиентов.
- Дизайн и архитектура: В дизайне и архитектуре нахождение доли числа позволяет определить пропорции и отношения различных элементов в создаваемом объекте или проекте.
- Спорт и физическая активность: В некоторых видах спорта доля числа используется для определения процентного соотношения успешных попыток, пульса или времени отдыха и тренировок.
- География: В географии нахождение доли числа позволяет определить площадь и объем территорий, а также пропорциональные отношения между географическими объектами.
Это лишь несколько примеров, в которых нахождение доли числа играет важную роль в реальной жизни. Знание и умение применять этот математический концепт может быть полезным в различных сферах деятельности.
Советы и рекомендации по нахождению доли числа при делении на дробь
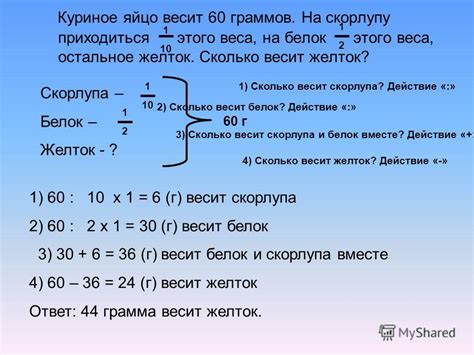
Вычисление доли числа при делении на дробь может показаться сложным, но с помощью нескольких советов и рекомендаций можно легко освоить эту операцию. Ниже представлены основные шаги, которые помогут вам правильно и точно найти долю числа.
Шаг 1: Сначала запишите дробь в форме десятичной дроби. Если дробь представлена в виде обыкновенной дроби, преобразуйте ее в десятичную форму, разделив числитель на знаменатель. Например, если у вас есть дробь 3/4, разделите 3 на 4 и получите 0.75.
Шаг 2: Затем умножьте десятичную дробь на исходное число, чтобы найти долю. Умножение число на десятичную дробь эквивалентно делению числа на обратную величину десятичной дроби. Например, если исходное число равно 10, и десятичная дробь равна 0.75, умножьте 10 на 0.75, чтобы получить долю числа.
Шаг 3: Выразите долю числа в виде десятичной или обыкновенной дроби, в зависимости от требований задачи.
Пример:
Предположим, что нужно найти долю числа 15 при делении на дробь 2/3.
Шаг 1: Преобразуем дробь 2/3 в десятичную форму. Делим 2 на 3 и получаем 0.6667 (округляем до четырех знаков после запятой).
Шаг 2: Умножаем число 15 на десятичную дробь 0.6667. Получаем 10.0005 (округляем до пяти знаков после запятой).
Шаг 3: Выражаем долю числа 15 в виде десятичной дроби: 10.0005.
Следуя этим простым советам и рекомендациям, вы сможете без труда находить долю числа при делении на дробь и успешно решать задачи связанные с этой операцией.