Как посчитать длину дуги окружности, зная только угол живота? Этот вопрос может быть актуальным для тех, кто занимается обработкой данных, геометрией или строительством. На первый взгляд может показаться, что это невозможная задача, но на самом деле она имеет простое решение.
Окружность - это фигура, которая обладает множеством интересных свойств. Один из таких параметров - ее длина. Дуга окружности - это часть окружности, ограниченная двумя точками.
Величина угла живота (или центрального угла) измеряется в градусах и указывает, насколько данный угол отклоняется от полной окружности (360 градусов). Чтобы найти длину дуги окружности по заданному углу, нам потребуется использовать формулу, которая связывает угол, радиус окружности и длину дуги.
Инструкции и советы по поиску дуги окружности по углу живота
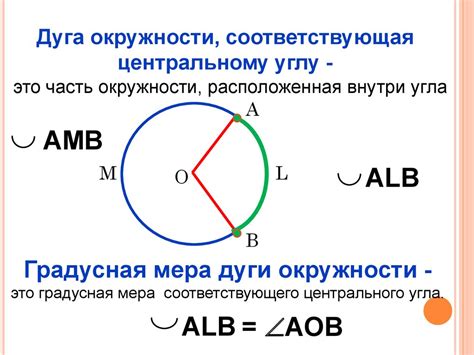
Поиск дуги окружности по углу живота может быть полезным для различных приложений, включая строительство и геодезию. В этом разделе мы предоставляем инструкции и советы по вычислению дуги окружности на основе заданного угла живота. Это поможет вам точно определить местоположение и размеры окружностей в ваших проектах.
Шаг 1: Подготовка данных
Перед началом расчетов убедитесь, что у вас есть все необходимые данные. Вам понадобится:
| Переменная | Описание |
| Угол живота | Заданный угол в градусах или радианах, измеренный от оси окружности |
| Радиус окружности | Расстояние от центра окружности до ее границы |
Шаг 2: Вычисление дуги окружности
Для вычисления дуги окружности по углу живота используйте следующую формулу:
Длина дуги = (угол живота / 360°) × 2π × радиус окружности
Здесь, π (пи) представляет собой математическую константу, примерное значение которой равно 3,14. Учтите, что угол живота должен быть в радианах для этой формулы. Если у вас есть угол живота в градусах, можете преобразовать его в радианы, используя формулу:
Угол (рад) = угол (град) × (π / 180°)
Советы и предупреждения
Некоторые дополнительные советы и предостережения, которые следует учесть при вычислении дуги окружности:
- Проверьте правильность измерений угла живота и радиуса окружности, чтобы избежать ошибок в расчетах.
- Используйте точные значения для π (пи), чтобы получить наиболее точные результаты.
- При использовании компьютерных программ или калькуляторов, убедитесь, что они используют правильные единицы измерения для угла (радианы) и радиуса (обычно метры или сантиметры).
- При работе с большими углами живота или малыми радиусами окружности, могут потребоваться дополнительные приближения или аппроксимации для более точных результатов.
Следуя этим инструкциям и советам, вы сможете легко вычислить дугу окружности по углу живота и применить эти знания в своих проектах и задачах.
Методы измерения угла живота
Измерение угла живота может быть полезным при решении различных задач, связанных с геометрией и физикой. Существует несколько методов, позволяющих определить угол живота.
1. Использование угломера. Угломер - это инструмент, предназначенный для измерения углов. Он состоит из шкалы и двух стрелок, которые указывают на угол. Для измерения угла живота необходимо положить угломер на предполагаемую дугу окружности и прочитать значение на шкале.
2. Использование протрахеалографии. Протрахеалография - это метод, основанный на измерении угла между прямыми и кривыми с помощью протрахеалографа. Протрахеалограф - это прибор, состоящий из двух стержней и системы шарниров. При помощи протрахеалографа можно измерить угол между стержнями и определить угол живота.
3. Использование тригонометрии. Тригонометрия - это раздел математики, который изучает связи между сторонами и углами в треугольниках. Для использования тригонометрии в измерении угла живота необходимо знать длину дуги окружности и радиус окружности. Зная эти значения, можно использовать тригонометрические функции для определения угла.
4. Использование специальных компьютерных программ и приложений. В современном мире существует множество программ и приложений, которые позволяют измерить угол живота с помощью специальных инструментов и алгоритмов. Такие программы могут быть полезными при решении сложных задач, требующих высокой точности измерений.
Выбор метода измерения угла живота зависит от конкретной ситуации и целей измерений. Каждый метод имеет свои преимущества и недостатки, поэтому важно выбрать наиболее подходящий метод для конкретной задачи.
Определение радиуса окружности по известному углу

Шаг 1: Измерьте угол живота. Это может быть угол между осью тела и прямым линейным отрезком от вашей талии до точки, где предполагается расположение центра окружности.
Шаг 2: Запишите измеренный угол в градусах.
Шаг 3: Используйте формулу для определения радиуса окружности по известному углу. Формула выглядит следующим образом: радиус = (длина дуги * 180) / (угол * 3,14). Длина дуги может быть выражена в сантиметрах.
Пример: Предположим, у вас измерен угол живота в 45 градусов, а длина дуги составляет 30 сантиметров. Тогда радиус окружности равен (30 * 180) / (45 * 3,14) = 57,32 сантиметра.
Обратите внимание, что эта формула представляет упрощенный подход к определению радиуса окружности по углу живота. Реальные результаты могут быть несколько искажены из-за различных факторов, таких как жировые отложения или аномалии анатомии. Поэтому рекомендуется проконсультироваться с врачом или специалистом перед использованием данной формулы для определения точного радиуса окружности.
Использование тригонометрических функций для расчета дуги окружности
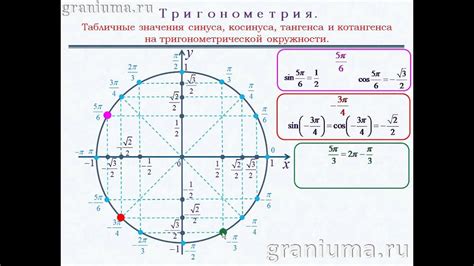
Для расчета дуги окружности по углу живота можно использовать тригонометрические функции, такие как синус и косинус. Для этого необходимо знать радиус окружности, а также значение угла живота в радианах.
Предположим, что у нас есть окружность радиусом R и угол живота α. Для расчета дуги окружности используется следующая формула:
длина дуги окружности = R * α
Однако, для использования этой формулы угол живота должен быть в радианах. Если угол указан в градусах, его необходимо преобразовать в радианы, используя следующую формулу:
α (в радианах) = α (в градусах) * π / 180
Для расчета дуги окружности можно использовать таблицу значений тригонометрических функций или калькулятор со встроенными тригонометрическими функциями. Например, чтобы найти синус угла живота, необходимо воспользоваться функцией sin(α), где α - угол живота в радианах.
Пользуясь этими простыми формулами и тригонометрическими функциями, вы сможете легко расчитать дугу окружности по углу живота и направлению его движения.
| Угол живота (α в градусах) | Угол живота (α в радианах) | Длина дуги окружности |
|---|---|---|
| 0° | 0 | 0 |
| 30° | π/6 | R * (π/6) |
| 45° | π/4 | R * (π/4) |
| 60° | π/3 | R * (π/3) |
| 90° | π/2 | R * (π/2) |
Преимущества использования геометрических методов при поиске дуги окружности

1. Точность измерений:
Геометрические методы позволяют получить наиболее точные измерения угла живота, что является важным при определении дуги окружности. Использование подходящих формул и методов гарантирует минимальную погрешность и точность результата.
2. Универсальность:
Геометрические методы применимы для поиска дуги окружности независимо от ее положения и размеров. Они позволяют работать с различными типами окружностей, в том числе с поверхностями разных форм, что повышает гибкость и универсальность алгоритма поиска.
3. Простота расчетов:
Геометрические методы обычно основаны на простых математических формулах, что делает их понятными и доступными для использования. Не требуется специальных знаний или сложных вычислений, что экономит время и ресурсы при поиске дуги окружности.
4. Возможность автоматизации:
Использование геометрических методов при поиске дуги окружности облегчает процесс автоматизации вычислений. Это позволяет разработать программное обеспечение или алгоритмы, которые могут самостоятельно определять дугу окружности по заданному углу живота с минимальным участием человека.
В результате использования геометрических методов при поиске дуги окружности получается более точный, универсальный, простой в использовании и автоматизируемый алгоритм, что значительно облегчает работу специалистов и повышает эффективность процесса.
Практическое применение формулы дуги окружности на примере задачи

Представьте себе задачу, в которой вам необходимо найти длину дуги окружности, зная только угол живота. Например, предположим, что у вас есть окружность радиусом 10 сантиметров, а угол живота составляет 45 градусов.
Для решения этой задачи можно воспользоваться формулой для нахождения длины дуги окружности:
L = 2πR (φ/360)
Где:
L - длина дуги окружности
π - математическая константа, примерное значение равно 3,14159
R - радиус окружности
φ - угол живота в градусах
В нашем примере:
L = 2π × 10 (45/360)
L ≈ 2π × 10 (0.125)
L ≈ 2π × 10 × 0.125
L ≈ 2π × 1.25
L ≈ 7.85 сантиметра
Таким образом, при угле живота 45 градусов длина дуги окружности радиусом 10 сантиметров составляет около 7.85 сантиметра.
Зная данную формулу, вы можете легко решать подобные задачи, опираясь на известные вам значения радиуса окружности и угла живота. Это особенно полезно при работе с геометрическими задачами или при проектировании различных форм и архитектурных элементов.
Инструменты и программы для автоматического расчета дуги окружности
Существует несколько инструментов и программ, которые могут помочь в автоматическом расчете дуги окружности по углу живота. Эти инструменты и программы предоставляют удобные функции и возможности для быстрого и точного определения дуги окружности.
Вот некоторые из наиболее популярных инструментов и программ, которые могут быть полезны при расчете дуги окружности:
- AutoCAD – профессиональная программа для автоматизированного проектирования и рисования, которая предоставляет возможность расчета дуги окружности с помощью математических формул и алгоритмов.
- Mathematica – компьютерная система алгебраических вычислений, которая содержит функции и операторы для расчета геометрических фигур, включая дуги окружности.
- Geogebra – бесплатная многофункциональная программа для математического моделирования и расчета графиков, которая предоставляет возможность расчета дуги окружности на основе заданных параметров.
- Wolfram Alpha – онлайн-сервис, который использует мощные алгоритмы и базу знаний, чтобы выполнять вычисления и предоставлять точные ответы на различные математические вопросы, включая расчет дуги окружности.
Эти инструменты и программы могут быть полезны для разных профессиональных областей, включая инженерное проектирование, архитектуру, математику и физику. Они облегчают и ускоряют процесс расчета дуги окружности, что позволяет экономить время и снижать вероятность возникновения ошибок.
Если вам необходимо регулярно выполнять расчеты дуг окружности, рекомендуется изучить возможности этих инструментов и программ, чтобы выбрать наиболее подходящий для ваших нужд. Помните, что квалифицированный специалист всегда может быть лучшим решением в сложных случаях, поэтому важно учитывать все факторы при выборе правильного метода расчета дуги окружности.
Рекомендации по проверке правильности найденной дуги окружности
После того, как вы успешно нашли дугу окружности по углу живота, рекомендуется провести проверку правильности полученных результатов. Это поможет избежать ошибок и убедиться в точности измерений. Вот несколько рекомендаций, которые помогут вам в этом:
1. Проверьте, что начальная и конечная точки дуги окружности действительно лежат на окружности. Убедитесь, что расстояние от каждой из этих точек до центра окружности равно радиусу окружности.
2. Измерьте длину дуги окружности с помощью специального инструмента или ленты. Сравните полученный результат с изначально найденной длиной дуги. Они должны быть примерно одинаковыми.
3. Проверьте правильность угла, по которому вы нашли дугу окружности. Убедитесь, что угол корректно измерен и соответствует действительному значению.
4. Проверьте, что дуга окружности плавно и равномерно изгибается в пределах угла, по которому вы нашли ее. Отсутствие резких переходов или деформаций говорит о правильности полученных результатов.
5. Если вы имеете доступ к другим методам измерения окружности, рекомендуется провести сравнительный анализ различных результатов. Это поможет подтвердить правильность ваших измерений.
Следование этим рекомендациям поможет вам удостовериться в правильности найденной дуги окружности. В случае сомнений или несоответствий, рекомендуется обратиться к специалисту для получения дополнительной поддержки и консультации.