Опорная окружность – это круг, касающийся окружности только в одной точке, называемой центром.
Дуга опорной окружности внешнего угла окружности позволяет нам определить угол между двумя лучами, выпускаемыми из центра окружности и касательной к этой окружности внешнему углу. Определение этого угла может быть полезно при решении различных геометрических задач.
Для нахождения дуги опорной окружности внешнего угла окружности нужно знать, что эта дуга равна половине суммы мер двух внутренних углов, образованных пересекающимися касательными.
Итак, если у вас есть окружность и внешний угол, и вы хотите найти дугу опорной окружности, следуйте установленной формуле: дуга опорной окружности внешнего угла равна половине суммы мер внутренних углов, образованных касательными.
Определение внешнего угла окружности
Для определения внешнего угла окружности необходимо знать радиус и координаты двух точек на окружности, через которые проводится линия, образующая данный угол. Подобрав соответствующие формулы для нахождения координат центра окружности и длины дуги, можно найти угол, используя геометрические свойства окружности.
Пример расчета внешнего угла окружности:
- Пусть координаты центра окружности равны (x0, y0), радиус окружности - R.
- Пусть точки A и B на окружности имеют координаты (x1, y1) и (x2, y2) соответственно.
- Находим длину дуги между точками A и B по формуле: L = R * α, где α - угол между точками A и B в радианах.
- Используя геометрические свойства окружности, находим внешний угол окружности: α = (L / R) * 180° / π.
Расчет внешнего угла окружности может быть полезен при решении геометрических задач и нахождении оптимальных углов для размещения объектов на плоскости окружности.
Значение дуги опорной окружности внешнего угла
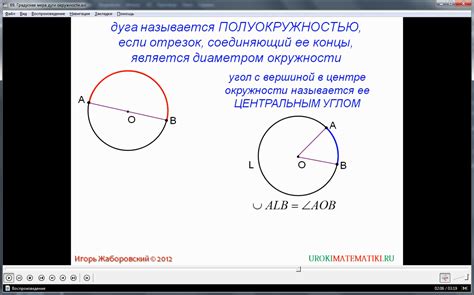
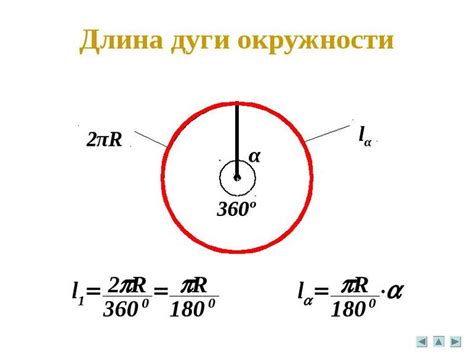
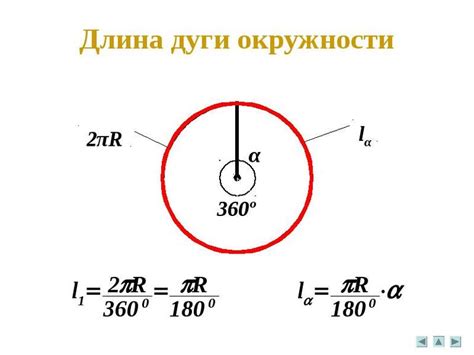
Как найти длину дуги опорной окружности внешнего угла? Для этого необходимо знать радиус окружности и величину внешнего угла. Длина дуги опорной окружности внешнего угла вычисляется по следующей формуле:
| Формула: | L = 2πR × (α / 360°) |
|---|---|
| где: | L - длина дуги опорной окружности внешнего угла |
| π - математическая константа (пи ≈ 3.14159) | |
| R - радиус окружности | |
| α - величина внешнего угла (в градусах) |
Например, если радиус окружности равен 5 сантиметрам, а величина внешнего угла равна 45 градусов, то длина дуги опорной окружности внешнего угла будет:
L = 2π × 5 × (45 / 360) ≈ 3.927 сантиметров.
Знание значения дуги опорной окружности внешнего угла может быть полезно при решении различных геометрических задач, а также при проектировании и расчёте конструкций, связанных с окружностями.
Формула для расчета дуги опорной окружности
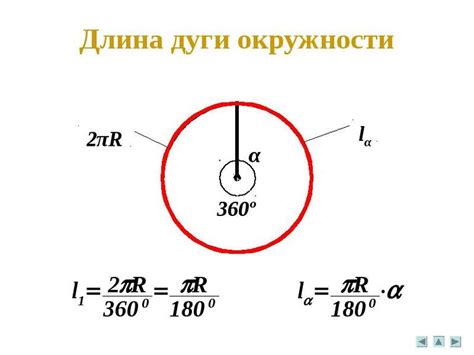
Для расчета дуги опорной окружности внешнего угла окружности существует простая и удобная формула.
Формула для расчета дуги опорной окружности состоит из двух частей:
- Находим длину дуги внешнего угла окружности по формуле:
Длина дуги = угол в градусах × радиус окружности × π / 180
Где:
- Длина дуги - искомое значение
- Угол в градусах - внешний угол окружности
- Радиус окружности - расстояние от центра окружности до внешнего угла
- π (или pi) - математическая константа, приближенное значение равно 3.14
Таким образом, вы можете использовать указанную формулу для точного и эффективного расчета дуги опорной окружности внешнего угла окружности.
Пример расчета дуги опорной окружности
Рассмотрим пример расчета дуги опорной окружности для внешнего угла окружности. Для начала, нам понадобятся значения радиусов и угла в градусах.
Пусть имеется окружность с радиусом R и внешним углом α. Необходимо найти длину дуги опорной окружности, которая образуется при продлении сторон окружности до пересечения внешним углом.
Для расчета длины дуги опорной окружности используется следующая формула:
| Формула: | L = 2πR(α/360) |
|---|
Где L - длина дуги опорной окружности, R - радиус окружности, α - внешний угол окружности в градусах.
Например, если радиус окружности составляет 5 см, а внешний угол равен 60 градусам, то длина дуги опорной окружности будет:
| Радиус окружности (R) | Внешний угол (α) | Длина дуги опорной окружности (L) |
|---|---|---|
| 5 см | 60 градусов | 5π/3 см |
Таким образом, длина дуги опорной окружности составляет 5π/3 см при данных значениях радиуса и внешнего угла.
Практические советы по поиску дуги опорной окружности
- Определите точку пересечения линии, проходящей через центр окружности и внешний угол, с самой окружностью. Эта точка будет являться одним из концов дуги опорной окружности.
- Создайте прямую, проходящую через эту точку и перпендикулярную к линии, проходящей через центр окружности и внешний угол. Эта прямая будет служить вам в качестве радиуса опорной окружности.
- Используя указанный радиус, проведите дугу опорной окружности, которая будет касаться самой окружности в двух точках: начальной и конечной.
Запомните, что для правильного определения дуги опорной окружности крайне важно точно измерить и построить все линии и углы. Не забывайте внимательно работать с геометрическими инструментами и быть внимательными к деталям.
Надеемся, что эти практические советы помогут вам успешно найти дугу опорной окружности внешнего угла окружности и решить задачи, связанные с геометрией.
Рекомендации по точному определению дуги опорной окружности
Определение дуги опорной окружности внешнего угла окружности может быть сложной задачей, но с правильным подходом и инструментами она может быть решена. Вот несколько рекомендаций, которые помогут вам достичь точности в этом процессе:
- Используйте соответствующие инструменты: Для определения дуги опорной окружности вам понадобится циркуль или другой инструмент с регулируемым радиусом. Убедитесь, что инструмент находится в хорошем состоянии и его радиус можно точно измерить.
- Следуйте математическим формулам: Управляя радиусом инструмента, следуйте формулам для определения дуги опорной окружности. Эти формулы зависят от радиуса внешней окружности и угла, в котором вы хотите определить дугу. Вы можете найти эти формулы в учебниках по геометрии или в интернете.
- Проверьте результаты: После определения дуги опорной окружности с помощью инструмента и математических формул, убедитесь, что результаты соответствуют вашим ожиданиям. Для этого вы можете использовать другие методы проверки или полагаться на ваши знания о геометрии.
- Будьте внимательными к деталям: В процессе определения дуги опорной окружности маленькие ошибки или неточности могут иметь значительное влияние на конечный результат. Поэтому будьте внимательны и осторожны при работе с инструментами и измерениями.
- Практикуйтесь: Как и в любой другой области, практика поможет вам улучшить навыки определения дуги опорной окружности. Уделите время для тренировок и экспериментов, чтобы стать более уверенным и точным в этом процессе.
Следуя этим рекомендациям, вы сможете точно определить дугу опорной окружности внешнего угла окружности. Помните, что практика и тщательность играют важную роль в достижении точности в геометрии.
Важность нахождения дуги опорной окружности внешнего угла окружности
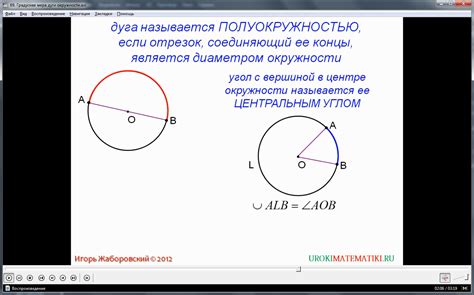
Дуга опорной окружности внешнего угла окружности представляет собой часть окружности, которая образует внешний угол с отрезком, соединяющим центр окружности с точкой пересечения окружности и касательной, проведенной из этой точки. Зная длину этой дуги, можно рассчитать площадь сектора, образованного этой дугой и радиусом окружности.
Важность нахождения дуги опорной окружности внешнего угла окружности заключается в том, что оно помогает в решении различных задач и приложений. Например, решение задачи на планиметрию, связанной с определением площади фигуры, образованной окружностью и ее взаимодействием с другими фигурами. Также, зная длину дуги опорной окружности, можно рассчитать ее длину с помощью формулы, а также найти угол, образованный этой дугой с радиусом.