Электродинамика – раздел физики, изучающий явления, связанные с движением заряженных частиц и электромагнитными полями. Один из важных аспектов этой науки – электромагнитная индукция. Она играет важную роль в различных технологиях и устройствах, таких как генераторы, электромоторы и трансформаторы.
ЭДС индукции – это явление, когда в закрытом электрическом контуре возникает электрическая разность потенциалов (ЭДС) под воздействием изменяющегося магнитного поля. Искать ЭДС индукции можно по формуле: ЭДС = -dφ/dt, где dφ/dt – производная изменения магнитного потока во времени. Отрицательный знак обусловлен законом Фарадея, гласящим, что положительное направление тока в контуре создает ЭДС, препятствующую изменению магнитного потока.
Как найти ЭДС индукции? Существуют несколько методов поиска, и все они основаны на принципе изменения магнитного поля во времени. Один из наиболее распространенных методов – использование закона Фарадея и определение величины ЭДС, возникающей в контуре при изменении магнитного потока. Также можно использовать правило правой руки и наблюдение эффекта индукции, исследуя поведение стрелки гальванометра или магнитного компаса.
Что такое ЭДС индукции

При изменении магнитного поля в контуре возникает электрическое поле, которое индуцирует движение электрических зарядов в контуре. Движение этих зарядов вызывает появление электрического напряжения, которое можно измерить с помощью вольтметра. Это и есть ЭДС индукции.
Закон Фарадея позволяет определить величину ЭДС индукции с помощью формулы:
- ЭДС индукции (E) = -n * ΔФ / Δt
где:
- E - электродвижущая сила, или ЭДС индукции (вольты)
- n - число витков контура
- ΔФ - изменение магнитного потока, пронизывающего контур (веберы)
- Δt - время, в течение которого происходит изменение магнитного потока (секунды)
Таким образом, ЭДС индукции позволяет нам преобразовывать энергию из магнитного поля в электрическую энергию и использовать ее в различных устройствах и системах.
Как работает контур
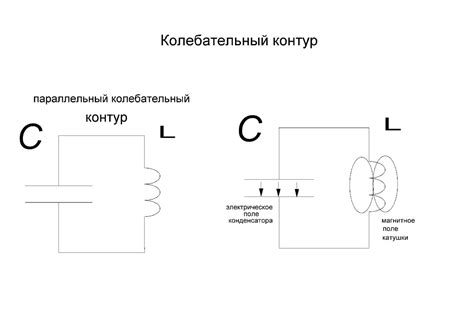
Основной принцип работы контура заключается в том, что изменяющийся магнитный поток, пронизывающий контур, вызывает появление эдс индукции в нем. Эдс индукции можно выразить с помощью формулы, которая выражает зависимость эдс от изменения магнитного потока и числа витков контура.
Для рассчета эдс индукции в контуре применяются различные методы, включая использование закона Фарадея и формулы Флеминга-леви. Также существуют специальные устройства и приборы, такие как индукционные катушки и трансформаторы, которые позволяют эффективно измерять и использовать эдс индукции в различных приложениях.
Важно отметить, что контур может быть как простым, состоящим из одного проводника, так и сложным, состоящим из нескольких проводников и элементов.
- В простом контуре эдс индукции можно рассчитать, используя формулу Эйнштейна-электромагнитной индукции.
- В сложном контуре необходимо учитывать взаимодействие различных элементов и проводников, что требует более сложных методов расчета и анализа.
Знание формул и методов расчета эдс индукции в контуре позволяет эффективно работать с различными электрическими системами и устройствами, такими как генераторы, трансформаторы, индукционные нагреватели и др.
Формула расчета эдс индукции
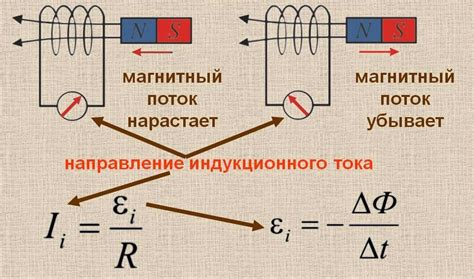
Эдс индукции представляет собой электромагнитную силу, возникающую в проводнике, когда он движется в магнитном поле или изменяется магнитное поле, пронизывающее его. Формула расчета эдс индукции в контуре основана на законе Фарадея электромагнитной индукции и имеет вид:
Э = -dФ/dt
где:
- Э - эдс индукции;
- dФ - изменение магнитного потока во времени;
- dt - время изменения магнитного потока.
Данная формула позволяет определить эдс индукции в любом контуре, на котором имеется изменение магнитного потока во времени.
Основными способами поиска эдс индукции в контуре являются:
- Подсчет изменения магнитного потока во времени и его производной.
- Использование закона Ленца - эдс индукции всегда направлена так, чтобы противостоять изменению магнитного потока.
- Использование правила правой руки - признаки движения проводника в магнитном поле и полярности эдс индукции можно определить с помощью правила правой руки.
Методы поиска эдс индукции в контуре

1. Закон Фарадея
Один из основных методов для расчета эдс индукции в контуре основан на законе Фарадея. Согласно этому закону, индуктивная ЭДС равна произведению изменения магнитного потока через контур на коэффициент самоиндукции контура:
ЭДС = -L * ΔΦ/Δt
где L - коэффициент самоиндукции контура, ΔΦ - изменение магнитного потока через контур, Δt - время, за которое происходит изменение магнитного потока. Знак "минус" в формуле указывает на то, что эдс индукции обратно пропорциональна изменению магнитного потока.
2. Правило Ленца
Для определения направления эдс индукции в контуре используется правило Ленца. Согласно этому правилу, эдс индукции всегда направлена так, чтобы ее действие противопоставлялось причине, вызывающей ее появление. Направление эдс индукции можно определить с помощью правила правой руки: если изображить большой палец правой руки по направлению магнитного поля, а остальные пальцы сокращенного кулака - по направлению контура, то направление эдс индукции будет соответствовать направлению большого пальца.
3. Использование интегральной формулы
Для более сложных случаев, когда магнитный поток через контур меняется неоднородно, можно использовать интегральную формулу:
ЭДС = -∮(E * dl)
где E - напряженность электромагнитного поля, dl - элемент длины контура. Интеграл берется по всему контуру. С помощью этой формулы можно определить эдс индукции в сложных геометрических формах контуров с изменяющимся магнитным полем.
Таким образом, методы поиска эдс индукции в контуре позволяют определить эту важную физическую величину и использовать ее при решении различных задач в электротехнике и физике.
Элементарные методы
Существует несколько элементарных методов для расчета ЭДС индукции в контуре. Рассмотрим некоторые из них:
- Метод изменения магнитного потока. В данном методе эдс индукции определяется как производная изменения магнитного потока по времени. Формула для расчета ЭДС по данному методу имеет вид: ε = -dΦ/dt, где ε - ЭДС индукции, dΦ - изменение магнитного потока, dt - изменение времени.
- Метод определения силы тока. Данный метод основывается на законе Ома, согласно которому сила тока в контуре равна отношению ЭДС индукции к сопротивлению контура. Формула для расчета ЭДС по данному методу имеет вид: ε = IR, где ε - ЭДС индукции, I - сила тока, R - сопротивление контура.
- Метод расчета по закону Фарадея. Данный метод основывается на законе Фарадея электромагнитной индукции, согласно которому эдс индукции равна произведению магнитной индукции поля на скорость изменения магнитного потока. Формула для расчета ЭДС по данному методу имеет вид: ε = Bvl, где ε - ЭДС индукции, B - магнитная индукция, v - скорость изменения магнитного потока, l - длина контура.
Вышеописанные методы являются простыми и позволяют сравнительно легко определить ЭДС индукции в контуре. Однако в некоторых сложных случаях требуется использование более сложных формул и методов для точного расчета ЭДС.
Метод внутреннего сопротивления
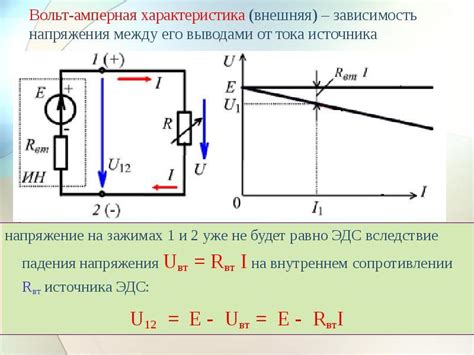
Внутреннее сопротивление источника электромагнитного поля является суммарным электрическим сопротивлением всех элементов контура, которые создают это поле. Оно включает в себя сопротивление проводов, элементов активных элементов (таких как генераторы, трансформаторы) и любых других сопротивлений, присутствующих в контуре.
Для расчета ЭДС индукции в контуре с использованием метода внутреннего сопротивления, можно использовать следующую формулу:
ЭДС = -L * di/dt - R * i,
где ЭДС - электродвижущая сила (ЭДС индукции), L - индуктивность контура, di/dt - изменение тока с течением времени, R - внутреннее сопротивление контура, i - ток в контуре.
С помощью метода внутреннего сопротивления можно определить ЭДС индукции в контуре, а также провести оценку влияния внутреннего сопротивления на работу контура.
Метод замкнутого контура

Для определения эдс индукции в замкнутом контуре применяется правило Ленца, которое гласит: направление индуцированного тока всегда таково, чтобы создавать магнитное поле, противодействующее изменению магнитного потока, вызванного внешним переменным магнитным полем.
Для расчета эдс индукции в замкнутом контуре можно использовать следующую формулу:
| Формула | Описание |
|---|---|
| ЭДС индукции (ε) | ε = -∫B·dl |
Где:
- ε - эдс индукции в контуре;
- B - магнитная индукция, создаваемая внешним магнитным полем;
- dl - элементарный участок контура.
Для нахождения эдс индукции необходимо пройти по всем участкам контура, и для каждого участка вычислить произведение магнитной индукции и элементарного участка.
Метод замкнутого контура позволяет учесть влияние каждого элементарного участка контура на эдс индукции. Таким образом, путем просмотра всего контура и складывания вкладов от каждого элементарного участка можно получить итоговую эдс индукцию в контуре.
Сложные методы

В поисках эдс индукции в контуре существуют не только простые, но и сложные методы расчета. Они требуют дополнительных усилий и знаний, но могут быть полезны для решения более сложных задач.
- Метод Стороженко: разработанный С. Стороженко, этот метод позволяет найти эдс индукции в контуре, используя закон Фарадея и закон Ома. Но для этого необходимо знать значения электрического сопротивления контура и силы тока, а также иметь данные об изменении магнитного потока во времени.
- Метод векторного потенциала: основанный на концепции векторного потенциала, этот метод позволяет найти эдс индукции в контуре, используя интеграл векторного потенциала по контуру. Этот метод требует использования векторного анализа и может быть сложным для понимания и применения.
- Метод разложения по собственным функциям: этот метод основан на разложении магнитного поля в контуре по собственным функциям. При использовании этого метода необходимо знать граничные условия и характеристики собственных функций, что делает его сложным для практического применения.
При использовании сложных методов расчета эдс индукции в контуре необходимо иметь подробные знания физики электромагнетизма. Но они могут быть полезны для решения сложных задач, требующих более точного расчета эдс индукции.
Метод графиков
Для применения метода графиков необходимо знать, как изменяется магнитный поток во времени и как связана с ним эдс индукции. Представим магнитный поток, пронизывающий контур, в виде графика Ф(t), где Ф - магнитный поток, а t - время. Затем, по этому графику, можно определить изменение магнитного потока во времени: dФ/dt.
Для определения эдс индукции в контуре используется формула: ЭДС = -dФ/dt, где dФ/dt - скорость изменения магнитного потока.
Далее строится временная зависимость эдс, то есть график ЭДС(t). По этому графику можно определить максимальное значение эдс в контуре, которое соответствует максимальной скорости изменения магнитного потока.
Таким образом, метод графиков позволяет определить эдс индукции в контуре, исходя из изменения магнитного потока во времени. Этот метод достаточно простой и наглядный, что делает его широко применимым при изучении электромагнетизма и расчете эдс в различных контурах.
Метод численных вычислений

Один из наиболее распространенных методов численных вычислений - метод прямоугольников, также известный как метод прямоугольной аппроксимации или метод левых прямоугольников. В этом методе вычисления осуществляются на основе аппроксимации подынтегральной функции прямоугольниками фиксированной ширины. Чтобы найти ЭДС индукции в контуре, следует разбить его на небольшие участки и приближенно вычислить интеграл для каждого из них. После этого, полученные значения суммируются.
Помимо метода прямоугольников, существуют и другие методы численных вычислений, такие как метод трапеций, метод Симпсона и др. Каждый из этих методов имеет свои особенности и применяется в зависимости от конкретной задачи.
Метод численных вычислений позволяет получить приближенное значение ЭДС индукции в контуре с высокой точностью, однако требует использования специальных алгоритмов и программного обеспечения для его реализации.
Таким образом, метод численных вычислений является важным инструментом для определения ЭДС индукции в контуре и находит широкое применение в научных и технических исследованиях.