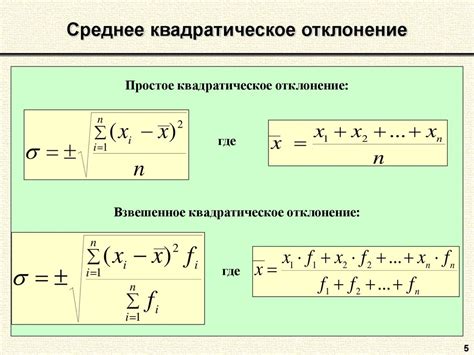
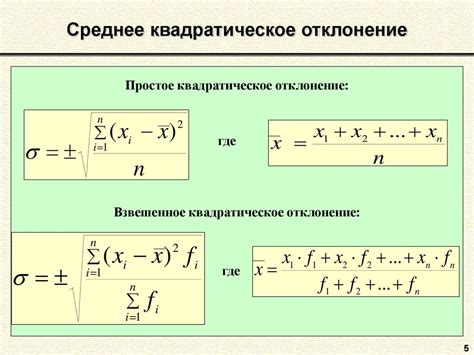
Абсолютное среднеквадратичное отклонение – это одна из основных характеристик, которая используется в физике для оценки разброса данных. Она позволяет определить, насколько рассеяны значения вокруг среднего. Знание этой формулы является необходимым для работы с физическими величинами и анализа экспериментальных данных.
Для нахождения абсолютного среднеквадратичного отклонения необходимо выполнить несколько шагов. Вначале нужно вычислить разность между каждым значением и средним значением выборки. Затем эти разности нужно возвести в квадрат. После этого необходимо найти среднее арифметическое полученных квадратов разностей. И наконец, извлечь квадратный корень из этого значения. Таким образом, получаем абсолютное среднеквадратичное отклонение.
Формула для вычисления абсолютного среднеквадратичного отклонения выглядит следующим образом:
σ = sqrt(Σ(x - x̄)² / N)
Где:
- σ – абсолютное среднеквадратичное отклонение
- Σ – сумма
- x – значение в выборке
- x̄ – среднее значение выборки
- N – количество значений в выборке
Используя данную формулу, можно точно определить абсолютное среднеквадратичное отклонение, что позволит более точно анализировать и интерпретировать экспериментальные данные в физике. Знание этой формулы является неотъемлемой частью физического образования и позволяет проводить точные измерения в научных исследованиях.
Формула абсолютного среднеквадратичного отклонения в физике
Δ = √[σ² + (δср)²],
где:
- Δ - абсолютное среднеквадратичное отклонение;
- σ - среднее квадратичное отклонение;
- δср - среднее отклонение от среднего значения.
Для вычисления абсолютного среднеквадратичного отклонения, необходимо предварительно определить среднее значение величины (Xср). Затем, для каждого измерения провести расчёты, определяя разницу между измеренным значением и средним значением (δ = X - Xср) и квадрат каждого значения δ (δ²). После чего вычислить среднее квадратичное отклонение (σ) и среднее отклонение от среднего значения (δср). Нахождение абсолютного среднеквадратичного отклонения выполняется подставлением полученных значений в формулу Δ = √[σ² + (δср)²].
Таким образом, абсолютное среднеквадратичное отклонение в физике используется для оценки точности и надёжности результатов исследований и экспериментов, а также для определения влияния случайных факторов на полученные данные.
Что такое абсолютное среднеквадратичное отклонение?

АСО является распространенной статистической характеристикой, которая позволяет определить, насколько значения в выборке отклоняются от среднего значения. Чем больше абсолютное среднеквадратичное отклонение, тем больший разброс данных можно ожидать.
Для вычисления АСО нужно выполнить следующие шаги:
- Вычислить среднее значение выборки.
- Вычислить разницу между каждым значением выборки и средним значением.
- Возвести каждую полученную разницу в квадрат.
- Найти среднее значение полученных квадратов.
- Извлечь квадратный корень из среднего значения полученных квадратов.
АСО предоставляет более полное представление о разбросе данных, чем просто среднее арифметическое отклонение. Оно учитывает как положительные, так и отрицательные значения отклонения и позволяет получить одну единицу измерения для характеристики точности данных.
Абсолютное среднеквадратичное отклонение находит применение во многих областях физики, таких как измерения в экспериментальной физике, обработка данных в физических моделях, оценка точности физических измерений и многое другое.
Формула абсолютного среднеквадратичного отклонения
Формула для расчета абсолютного среднеквадратичного отклонения в физике имеет следующий вид:
σ = √(∑|xi - x̅|² / n)
Где:
- σ - абсолютное среднеквадратичное отклонение;
- ∑ - сумма всех значений в выборке;
- |xi - x̅| - модуль разности между каждым значением выборки и средним значением выборки (модуль отклонения каждого значения от среднего);
- n - количество значений в выборке.
Формула позволяет найти среднеквадратичное отклонение с учетом абсолютных значений отклонений каждого значения от среднего. Это позволяет учесть величину отклонений независимо от их направления и получить полную картину разброса данных.
Абсолютное среднеквадратичное отклонение является важным инструментом в физике, позволяющим оценить точность измерений, проверить стабильность результатов и сравнить различные наборы данных.
Примечание: Формула может быть модифицирована в зависимости от конкретного случая и вида данных.
Пример расчета абсолютного среднеквадратичного отклонения

Представим, что проводится эксперимент по измерению длины стержня. В ходе эксперимента было проведено 5 измерений, и получены следующие результаты: 12.1 см, 12.5 см, 11.9 см, 12.3 см, 12.2 см. Чтобы найти АСКО по этим данным, выполним следующие шаги:
1. Вычислим среднее значение измерений. Просуммируем все измерения и поделим их на количество измерений:
12.1 см + 12.5 см + 11.9 см + 12.3 см + 12.2 см = 60 см
60 см / 5 = 12 см
Среднее значение измерений равно 12 см.
2. Вычислим отклонение каждого измерения от среднего значения. Для этого вычтем среднее значение из каждого измерения:
12.1 см - 12 см = 0.1 см
12.5 см - 12 см = 0.5 см
11.9 см - 12 см = -0.1 см
12.3 см - 12 см = 0.3 см
12.2 см - 12 см = 0.2 см
3. Возьмем абсолютное значение отклонения из каждого измерения:
|0.1 см| = 0.1 см
|0.5 см| = 0.5 см
| -0.1 см| = 0.1 см
|0.3 см| = 0.3 см
|0.2 см| = 0.2 см
4. Найдем сумму абсолютных отклонений:
0.1 см + 0.5 см + 0.1 см + 0.3 см + 0.2 см = 1.2 см
5. Разделим сумму абсолютных отклонений на количество измерений:
1.2 см / 5 = 0.24 см
Абсолютное среднеквадратичное отклонение равно 0.24 см.
Таким образом, в данном примере АСКО составляет 0.24 см, что может означать, что измерения проведены с достаточной точностью.