Цилиндр – это геометрическое тело, обладающее высотой, радиусом и двумя плоскими гранями, которые являются окружностями. Определение сечения цилиндра – это важный этап в изучении и расчетах данной фигуры, и существует несколько методов и подходов, которые позволяют найти формулу для этого.
Один из самых простых и распространенных методов – это использование геометрических свойств цилиндра. В основе такого подхода лежит изучение круговых сечений, которые образуются плоскостью, пересекающей цилиндр. Такие сечения могут быть окружностями либо эллипсами в зависимости от направления плоскости и отношения между радиусами основания цилиндра и сечения.
Для нахождения формулы сечения цилиндра направленной плоскостью необходимо учесть следующие факторы: расположение плоскости относительно оси цилиндра, угол между плоскостью и поперечным сечением, а также смещение плоскости относительно основания цилиндра. При помощи геометрических методов (например, теоремы Пифагора или теоремы косинусов) можно вывести формулы для нахождения радиуса и координат центра сечения цилиндра.
Математические методы для определения сечения цилиндра
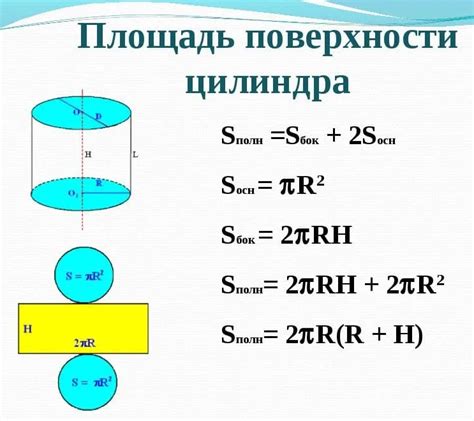
Существует несколько математических методов для определения сечения цилиндра. Один из них основан на использовании геометрии и требует знания основных формул и правил. Другие методы используют исчисление и алгебру для нахождения точных значений сечения.
В геометрии для определения сечения цилиндра применяются такие формулы, как площадь круга, площадь прямоугольника и площадь параллелограмма. Эти формулы помогают найти площадь сечения цилиндра и его характеристики, такие как радиус или диаметр. Они также позволяют определить другие параметры, такие как объем или общая площадь поверхности цилиндра.
Для применения методов исчисления и алгебры для определения сечения цилиндра необходимо выразить его формулу в алгебраической форме. Затем можно найти точки пересечения с плоскостью и использовать методы исчисления для нахождения точных значений.
Помимо этих основных методов, существуют и более сложные математические подходы для определения сечения цилиндра. Они включают в себя использование векторов и матриц, численные методы, преобразование Фурье и теорию графов. Эти методы требуют более глубоких знаний математики и часто применяются в научных и исследовательских работах.
Геометрический подход к определению сечения цилиндра

Геометрический подход к определению сечения цилиндра заключается в использовании основных принципов и свойств геометрии. Для определения сечения цилиндра требуется задать плоскость, которая будет пересекать цилиндр. Эту плоскость можно задать различными способами, например, указав точку и нормальный вектор плоскости или указав три точки, через которые проходит плоскость.
После задания плоскости, определяющей сечение цилиндра, необходимо определить точки пересечения плоскости с поверхностью цилиндра. Для этого можно воспользоваться математическими операциями и уравнениями, которые описывают геометрическую форму цилиндра. Найдя точки пересечения, можно построить границы сечения цилиндра.
Дополнительно, при геометрическом подходе к определению сечения цилиндра, можно учитывать различные параметры и характеристики цилиндра, такие как радиус основания, высота цилиндра и угол наклона списка, которые могут оказать влияние на форму и размер сечения цилиндра.
Геометрический подход к определению сечения цилиндра предоставляет широкие возможности для получения точных и полных результатов. Он может быть использован в различных областях, таких как инженерия, архитектура, физика и многие другие. Правильное определение сечения цилиндра позволяет учесть особенности формы и размера, а также применить ее в практических задачах и исследованиях.
Определение сечения цилиндра с помощью формулы объема
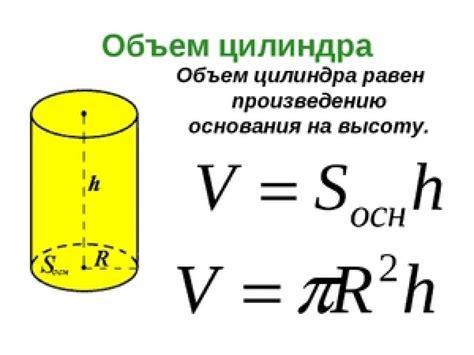
Для определения сечения цилиндра с помощью формулы объема необходимо знать радиус основания цилиндра и высоту цилиндра. Формула объема цилиндра выглядит следующим образом:
V = πr^2h
где V – объем цилиндра, π – математическая константа, примерное значение которой равно 3,14159, r – радиус основания цилиндра и h – высота цилиндра.
Если известны значения объема цилиндра и высоты цилиндра, можно использовать данную формулу для определения радиуса основания цилиндра. Для этого необходимо перейти к формуле вида:
r = √(V / (πh))
Таким образом, формула объема цилиндра может быть использована для определения сечения цилиндра на основе известных значений радиуса основания, высоты или объема цилиндра. Она позволяет найти одну из величин при известных двух.
Теорема Пифагора и ее использование для определения сечения цилиндра

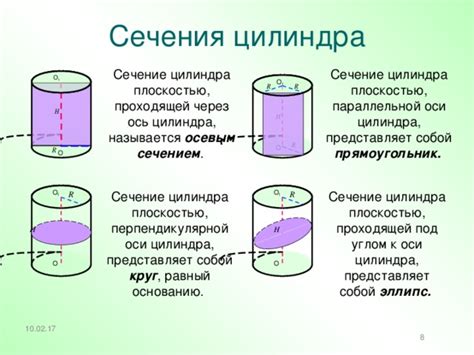
Сечение цилиндра - это плоская фигура, полученная путем пересечения цилиндрической поверхности плоскостью, не параллельной его оси. Чтобы найти формулу для определения сечения цилиндра, можно использовать теорему Пифагора. Представим, что плоскость сечения разделяет цилиндр на два участка - верхний и нижний. Для нахождения формулы, нам необходимо знать длину радиуса цилиндра (r), расстояние от плоскости сечения до оси цилиндра (h), и длину линии сечения (c).
Согласно теореме Пифагора, в прямоугольном треугольнике с катетами a и b и гипотенузой c выполняется следующее соотношение: a^2 + b^2 = c^2. Применяя эту теорему к нашему сечению цилиндра, мы можем вывести следующую формулу:
(r-h)^2 + c^2 = r^2
Где r - радиус цилиндра, h - расстояние от плоскости сечения до оси цилиндра, а c - длина линии сечения.
Используя данную формулу, можно легко вычислить сечение цилиндра, зная значения радиуса, расстояния до оси и длины линии сечения. Таким образом, теорема Пифагора представляет собой полезный инструмент для определения сечения цилиндра и применяется в различных областях, где требуется работа с цилиндрическими фигурами.
Альтернативные методы определения сечения цилиндра: графический и численный подходы
Графический подход заключается в построении графика функции, описывающей сечение цилиндра, и определении площади под кривой на этом графике. Для этого можно использовать специальные программы или рисовать график вручную с использованием координатной плоскости. Этот метод позволяет получить графическую интерпретацию сечения цилиндра и может быть полезен при изучении его формы и свойств.
Численный подход основан на применении численных методов для приближенного вычисления площади сечения цилиндра. Один из таких методов – метод Монте-Карло, который основывается на генерации случайных точек внутри заданной области и подсчете доли точек, попавших в сечение цилиндра. Чем больше точек используется, тем точнее будет полученный результат.
Оба альтернативных метода имеют свои преимущества и недостатки. Графический подход позволяет визуализировать сечение цилиндра и получить графическое представление его формы. Однако этот метод требует тщательного и аккуратного проведения графика, что может быть затруднительно при работе с большими наборами данных.
Численный подход, в свою очередь, обеспечивает быстрое и приближенное вычисление площади сечения цилиндра, но может потребовать большого количества вычислительных ресурсов при использовании большого количества точек.
Выбор конкретного метода определения сечения цилиндра зависит от задачи и требуемой точности результата. В некоторых случаях может быть полезно использовать комбинацию графического и численного анализа для достижения наиболее точного и наглядного результата.