Трапеция - это четырехугольник, у которого две стороны параллельны. Одна из оснований трапеции называется меньшим, а другая - большим. Восьмиклассники учатся находить длину основания трапеции и это становится одной из первых задач по геометрии, с которыми им приходится столкнуться. Это важное умение, поскольку знание формулы для нахождения основания трапеции позволяет решать более сложные задачи и строить графики функций.
Формула для нахождения длины основания трапеции может быть различной, в зависимости от того, какие данные даны в задаче. Однако наиболее часто используемая формула основана на применении свойства параллельных линий. Если AB и CD - параллельные стороны трапеции, а BC и AD - основания, то можно записать, что отношение длин AC и BD равно отношению длин AB и CD.
Таким образом, формула для нахождения длины основания трапеции может быть записана как: BC = (CD * AC) / AB. Здесь BC - длина одного из оснований трапеции, CD и AB - длины параллельных сторон, а AC и BD - диагонали трапеции, которые можно измерить или выразить через другие известные величины. Пример использования этой формулы будет наглядно показан ниже.
Основание трапеции: формула для 8 класса
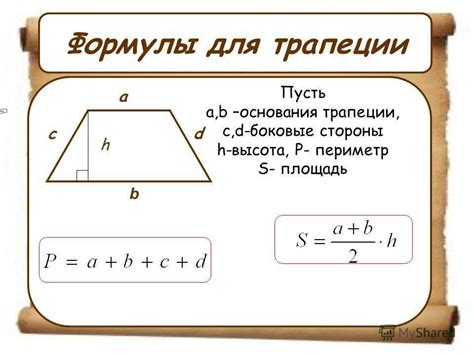
Формула для вычисления основания трапеции зависит от доступных данных:
1. Если известны длины боковых сторон (a и b) и диагонали (d1 и d2), можно воспользоваться следующей формулой:
Основание трапеции = [(d1 + d2) - (b - a)] / 2
2. Если известны длины боковых сторон (a и b) и высота (h), формула для вычисления основания будет следующей:
Основание трапеции = [(a + b) * h] / 2
3. Если известны только длины боковых сторон (a и b), формула для вычисления основания будет следующей:
Основание трапеции = (a + b) / 2
Помните, что в 8 классе основная цель изучения формулы для основания трапеции - развитие навыков решения задач и понимание закономерностей в геометрии. Также важно научиться анализировать и применять предоставленные данные для нахождения правильного ответа.
Что такое трапеция?
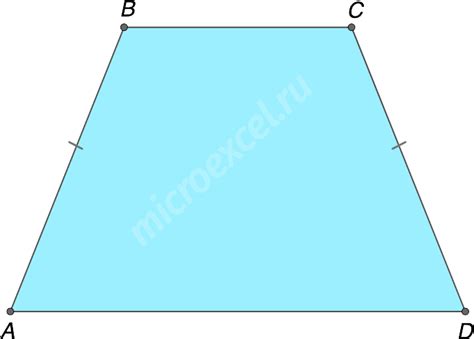
Основание трапеции - это отрезок, соединяющий две противоположные вершины. Оно может быть как горизонтальным, так и наклонным. Наклонное основание называется "асиметричной" трапецией, а горизонтальное основание - "симметричной" трапецией.
Трапеция имеет несколько особенностей:
- Сумма всех углов внутри трапеции всегда равна 360 градусов.
- Углы, лежащие на одной стороне трапеции, называются "смежными углами". Они всегда сумма равна 180 градусов.
- Периметр трапеции равен сумме длин всех её сторон.
- Площадь трапеции можно найти, используя формулу: площадь = (сумма оснований * высота) / 2.
Узнавая эти особенности, мы можем легко находить различные параметры и свойства трапеции, а также использовать их для решения задач.
Определение основания трапеции
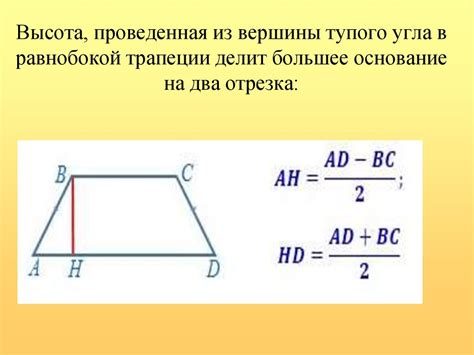
Трапеция имеет два основания, которые могут быть разной длины.
Для нахождения основания трапеции можно использовать следующие способы:
- Если известны длины боковых сторон и высоты трапеции, можно использовать формулу для нахождения площади: S = (a + b) * h / 2, где a и b - длины оснований, h - высота.
- Если известны длины диагоналей и углы при основаниях, можно использовать теорему косинусов: a^2 = b^2 + c^2 - 2bc * cos(A), где a и c - длины диагоналей, b - разность между длинами оснований, A - угол между диагоналями.
- Если известны длины боковых сторон и углы при основаниях, можно использовать некоторые другие формулы и свойства трапеции, например, теорему синусов.
Основание трапеции является одним из ее главных элементов, влияющих на ее свойства, формулы и способы вычисления площади, периметра и других характеристик.
Как найти длину основания?
Если известны длины двух оснований трапеции, то можно просто сложить их и разделить полученную сумму на 2. Таким образом, формула для нахождения длины основания t выглядит следующим образом:
t = (a + b) / 2
где a и b - длины оснований трапеции.
Если известны длины боковых сторон трапеции и диагоналей, можно воспользоваться теоремой Пифагора для нахождения длины основания. Для этого нужно выполнить следующие шаги:
- Найдите квадраты длин боковых сторон и сложите их: c^2 = a^2 + b^2.
- Найдите квадраты длин диагоналей и сложите их: d^2 = c^2 + t^2.
- Выразите длину основания: t = sqrt(d^2 - c^2).
После выполнения этих шагов можно найти длину основания t.
Используя эти методы и формулы, можно легко найти длину основания трапеции и успешно решать геометрические задачи на эту тему.
Формула для нахождения основания трапеции
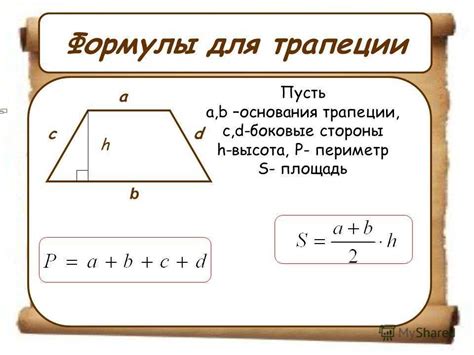
Если известны длины боковых сторон трапеции и диагонали, то размер основания можно найти по следующей формуле:
- Найдите полупериметр трапеции, сложив длины всех её сторон и разделив полученную сумму на 2.
- Используя формулу Герона, найдите площадь трапеции.
- Далее, выразите длину основания через площадь и диагональ трапеции по следующей формуле:
основание = (площадь * 2) / (диагональ)
Таким образом, зная длины боковых сторон трапеции и длину её диагонали, можно легко найти размер основания по указанной формуле.
Пример вычисления основания трапеции
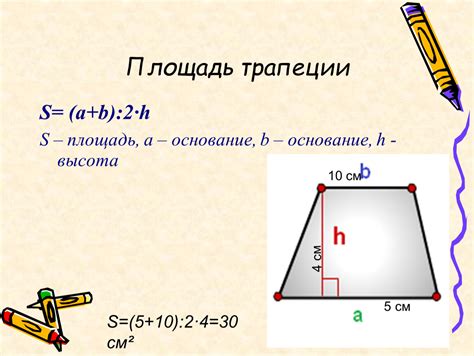
Для того чтобы найти основание трапеции, нужно знать длины боковых сторон и высоту.
Рассмотрим пример. Пусть дана трапеция ABCD, где AB и CD - основания трапеции, AC и BD - боковые стороны, и h - высота трапеции.
Дано: AB = 6 см, CD = 10 см, h = 4 см
| Сторона | Длина (см) |
|---|---|
| AB | 6 |
| CD | 10 |
| AC | ? |
| BD | ? |
Для вычисления основания трапеции AC и BD можно воспользоваться теоремой Пифагора, так как в трапеции AC и BD являются диагоналями. Для вычисления AC применим теорему Пифагора к треугольнику ABC:
AC2 = AB2 + BC2
AC2 = 62 + BC2
AC2 = 36 + BC2
AC2 - BC2 = 36
Точно также можем найти BD. Для этого применим теорему Пифагора к треугольнику BCD:
BD2 = BC2 + CD2
BD2 = BC2 + 102
BD2 = BC2 + 100
Итак, мы имеем систему уравнений:
AC2 - BC2 = 36
BD2 = BC2 + 100
Решая данную систему, находим значение BC, которое является основанием трапеции:
36 - BC2 = BC2 + 100
2BC2 = -64
BC2 = -32
Мы получили отрицательный результат, который не имеет смысла с точки зрения геометрии. Это значит, что указанные значения сторон и высоты не образуют реальную трапецию.
Важно помнить, что для корректного вычисления основания трапеции, необходимо иметь правильные значения сторон и высоты.
Практическое применение формулы

Формула для нахождения основания трапеции имеет практическое применение в различных ситуациях. Одной из таких ситуаций может быть расчет площади поверхности трапеции.
Например, если у вас есть трапеция с известными значениями высоты и длин боковых сторон, вы можете использовать формулу для нахождения основания трапеции, чтобы рассчитать площадь этой фигуры. Зная значения этих параметров, вы сможете с легкостью применить формулу и получить точное значение площади трапеции.
Также формула может быть использована для определения длины основания трапеции в различных задачах. Например, если у вас есть данные о площади трапеции и высоте, вы можете использовать формулу для нахождения длины основания трапеции.
Практическое применение формулы для нахождения основания трапеции может быть полезным в различных областях, таких как архитектура, геометрия, строительство и т.д. Знание этой формулы поможет вам решить задачи, связанные с трапециями, и упростит вашу работу в этих областях.
В данной статье мы рассмотрели основание трапеции и проанализировали формулу для его нахождения. Основание трапеции представляет собой отрезок, соединяющий две противоположные вершины. Для нахождения длины основания трапеции, нам понадобилось знать длины сторон трапеции и диагонали. С помощью этих данных мы смогли определить формулу для нахождения основания трапеции.
Формула для нахождения основания трапеции: основание = (сумма длин диагоналей - разность длин боковых сторон) / 2.
Теперь мы можем легко определить длину основания трапеции, если у нас есть все необходимые данные. Это позволит нам решать задачи, связанные с трапециями, более эффективно и точно.
Таким образом, знание формулы для нахождения основания трапеции является важным элементом в изучении геометрии и помогает нам лучше понимать особенности этой фигуры.