Косинус - одна из основных тригонометрических функций, которая широко используется в математике, физике и инженерных науках. Она позволяет определить угловые отношения в треугольниках и круговых функциях. Изучение косинуса угла и его формулы имеет особое значение для решения различных задач, связанных с геометрией, физикой и компьютерным моделированием.
Формула косинуса угла является одной из основных формул тригонометрии и связывает значения сторон треугольника с косинусом напротив угла. Она может быть записана в виде:
cos α = c / a
где α - угол между сторонами a и c. Формулу косинуса угла можно использовать для нахождения угла, если известны значения сторон треугольника, а также для нахождения длины стороны, если известны значения двух других сторон и угла между ними.
Знание формулы косинуса угла играет важную роль при решении задач, связанных с определением расстояний, углов, высот и других характеристик треугольников. Оно также находит применение в различных областях науки и техники, таких как астрономия, геодезия, физика и компьютерная графика.
Определение угловых отношений

Одной из основных формул, используемых для определения угловых отношений, является формула косинуса угла. Косинус угла можно выразить как отношение длины прилежащего катета к гипотенузе прямоугольного треугольника.
Формула косинуса угла выглядит следующим образом:
| Косинус угла: | cos(α) = a / c |
Где:
- α - угол;
- a - прилежащий катет;
- c - гипотенуза.
Использование формулы косинуса позволяет определить угловые отношения и решать задачи, связанные с треугольниками, например, нахождение неизвестного угла или стороны треугольника.
Зная формулу косинуса и значения известных сторон треугольника, можно вычислить значение угла при помощи обратной функции косинуса – арккосинуса.
Определение угловых отношений и использование соответствующих формул позволяют решать разнообразные геометрические задачи и производить точные расчеты в различных областях науки и техники.
Тригонометрические функции и их применение
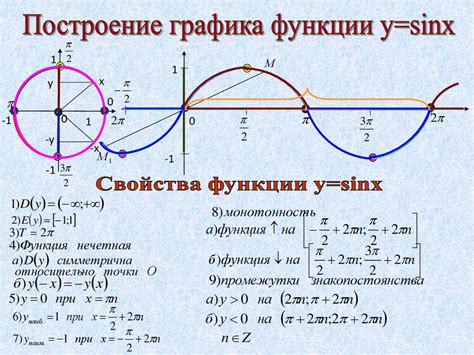
Самая известная тригонометрическая функция – это синус, обозначаемый символом sin. Он определяется как отношение противоположной стороны к гипотенузе треугольника. Также существуют косинус, обозначаемый символом cos, тангенс (tg), котангенс (ctg), секанс (sec) и косеканс (cosec).
Тригонометрические функции широко используются в различных областях науки и инженерии. Они помогают решать задачи, связанные с измерением углов, расчетами векторов и фазовыми диаграммами.
Применение тригонометрии часто встречается в физике, например, для расчета длин волн света, изучения движения частиц и вычисления силы тяжести. В геометрии тригонометрия помогает находить длины сторон и углы треугольников. В инженерии тригонометрические функции используются, например, при построении графиков сигналов и анализе колебаний. Также тригонометрия полезна при решении задач навигации, астрономии, строительства и дизайна.
Одной из важных формул тригонометрии является формула косинуса угла. Она позволяет определить угловые отношения и находить длины сторон треугольника по заданным углам и сторонам. Формула косинуса угла выглядит следующим образом:
cos(α) = c / a
где α – заданный угол треугольника, с – длина стороны, соседней к углу α, a – длина гипотенузы треугольника.
Использование формулы косинуса угла позволяет решать разнообразные задачи, связанные с треугольниками, такие как нахождение углов, сторон, высот и площадей треугольников. Она широко применяется в геометрии, физике, инженерии и других областях науки.
Виды тригонометрических функций
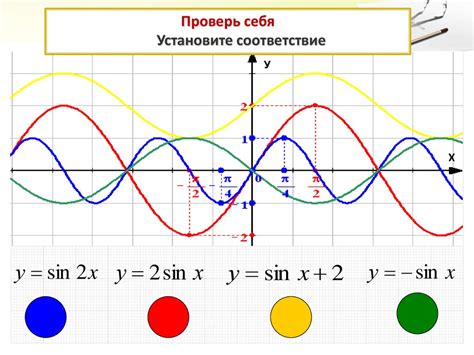
Косинус - это одна из основных тригонометрических функций, которая используется для определения отношения длины прилежащего катета к гипотенузе прямоугольного треугольника. Функция косинуса обозначается как cos(α), где α - угол, а соответствующее значение функции косинуса представляет собой отношение длины прилежащего катета к гипотенузе.
| Название функции | Обозначение | Определение |
|---|---|---|
| Синус | sin(α) | Противоположный катет / Гипотенуза |
| Косинус | cos(α) | Прилежащий катет / Гипотенуза |
| Тангенс | tan(α) | Противоположный катет / Прилежащий катет |
| Котангенс | cot(α) | Прилежащий катет / Противоположный катет |
| Секанс | sec(α) | Гипотенуза / Прилежащий катет |
| Косеканс | csc(α) | Гипотенуза / Противоположный катет |
Все эти функции могут быть выражены с помощью экспоненциальной формы, тригонометрическим и функциональным тождествам. Они играют важную роль в различных ветвях математики и научных дисциплинах, включая физику, инженерию, астрономию и др.
Соотношения между тригонометрическими функциями

Формула косинуса угла позволяет определить косинус данного угла, исходя из соответствующих сторон треугольника. Она выглядит следующим образом:
cos(α) = смежная сторона / гипотенуза
где α - угол, смежная сторона - сторона треугольника, лежащая рядом с данным углом, а гипотенуза - сторона, лежащая напротив прямого угла.
Формула косинуса угла является одной из основных формул тригонометрии и находит широкое применение в решении геометрических задач, а также в физике, инженерии и других науках.
Углы и их измерение
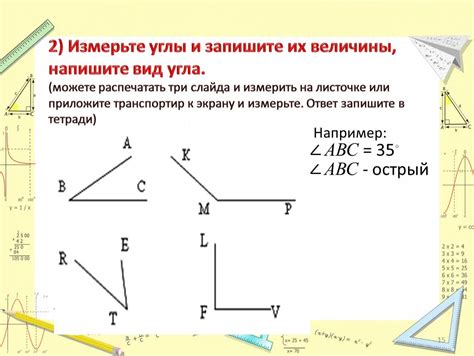
Существует несколько способов измерения углов:
- Градусы: угол делится на 360 равных частей, каждая из которых называется одним градусом.
- Минуты: градус делится на 60 минут, каждая из которых равна 1/60 градуса.
- Секунды: минута делится на 60 секунд, каждая из которых равна 1/60 минуты или 1/3600 градуса.
Угол может быть положительным или отрицательным, в зависимости от направления его вращения. Положительный угол вращается против часовой стрелки, а отрицательный – по часовой стрелке.
Измерение углов позволяет определить их величину и сравнивать между собой. Знание угловых отношений позволяет решать множество задач в геометрии и тригонометрии, а также применять их в различных областях науки и техники.
Формула косинуса угла

Формула косинуса угла имеет следующий вид:
cos(α) = a / c
где α - мера угла, a - длина стороны, противолежащей углу α, и c - длина гипотенузы.
Формула косинуса угла позволяет рассчитать значение косинуса угла по известным значениям стороны и гипотенузы. Это может быть полезно при решении задач, связанных с определением угла в треугольнике.
Для использования формулы косинуса угла необходимо знать значения длин стороны и гипотенузы. После вычисления косинуса угла можно применять его для определения других угловых отношений, таких как синус, тангенс и котангенс.
Применение формулы косинуса угла

Формула косинуса угла очень полезна для определения угловых отношений и находит широкое применение в различных областях, включая геометрию, физику, инженерию и компьютерную графику.
Одним из основных применений формулы косинуса является нахождение длины стороны треугольника, если известны длины двух других сторон и величина внутреннего угла. Это может быть полезно, например, при измерении расстояний на карте или в реальном мире.
Формула косинуса также позволяет определить значение угла между двумя сторонами треугольника, если известны длины всех трех сторон. Это может быть полезно, например, при решении задач, связанных с направлением движения или определением ориентации объектов.
В физике формула косинуса используется для определения силы или вектора, действующего под определенным углом. Она также может быть использована для нахождения компонентов вектора по разным осям координатной системы.
В компьютерной графике формула косинуса используется для определения взаимного расположения объектов или для создания эффектов визуализации, связанных с трехмерной графикой.
Таким образом, формула косинуса угла является важным инструментом для решения различных задач, связанных с угловыми отношениями. Она находит применение во многих областях и является одной из основных формул, используемых для работы с углами.