Как найти гипотенузу через синус и косинус пошагово — объяснение и примеры

Гипотенуза – это сторона треугольника, противолежащая прямому углу. Она является самой длинной стороной и обозначается буквой c. Но как найти ее значение, если известны значения синуса и косинуса углов треугольника?

Для начала, нужно знать определение синуса и косинуса. Синус (sin) угла равен отношению противолежащей стороны к гипотенузе, а косинус (cos) угла равен отношению прилежащей стороны к гипотенузе.

Чтобы найти гипотенузу, используем формулу:

c = |a / sinA|

Здесь a – сторона, противолежащая углу A. Проще говоря, для нахождения гипотенузы нужно разделить длину стороны, противолежащей углу, на значение синуса этого угла.

Теперь рассмотрим пример. Пусть у нас есть треугольник ABC, в котором известны угол A и сторона a:

Допустим, угол A равен 45 градусов, а сторона a равна 3. Чтобы найти гипотенузу c, используем формулу:

c = |3 / sin45°|

Выполняем расчет:

c = 3 / 0.7071 ≈ 4.24

Таким образом, гипотенуза треугольника ABC примерно равна 4.24 единицы длины.

Теперь ты знаешь, как найти гипотенузу через синус и косинус пошагово. Этот метод очень полезен при решении задач из геометрии и тригонометрии, особенно когда известны значения синуса и косинуса углов треугольника.

Определение гипотенузы через синус и косинус

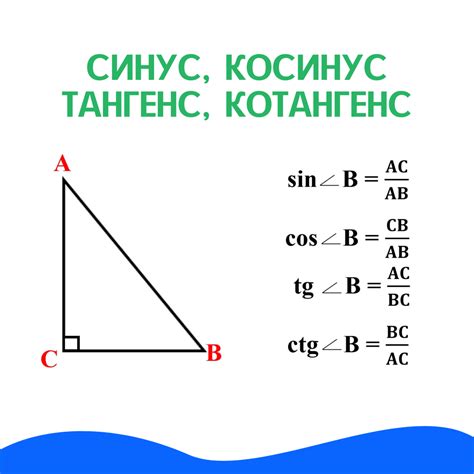
Для определения гипотенузы через синус и косинус, нужно знать длину одной из катетов и меру угла между гипотенузой и этим катетом. По определению, синус угла в прямоугольном треугольнике равен отношению противоположего катета к гипотенузе, а косинус угла равен отношению прилежащего катета к гипотенузе.

Для нахождения гипотенузы пошагово можно использовать следующую формулу:

гипотенуза = катет / косинус угла

Или аналогично:

гипотенуза = катет / синус угла

Таким образом, зная длину катета и значение синуса или косинуса угла, можно вычислить длину гипотенузы.

Пример:

Допустим, у нас есть прямоугольный треугольник, в котором один катет равен 5 и угол между гипотенузой и этим катетом равен 30 градусам.

Для начала, найдем значение косинуса угла 30 градусов. Косинус 30 градусов равен 0.866 (округленно).

Теперь мы можем использовать формулу, чтобы найти гипотенузу:

гипотенуза = 5 / 0.866 ≈ 5.774

Таким образом, длина гипотенузы примерно равна 5.774 в данном примере.

Шаг 1: Находим значения синуса и косинуса

Перед тем как найти гипотенузу по синусу и косинусу, необходимо определить значения этих тригонометрических функций. Для этого необходимо знать длины противолежащего и прилежащего катетов в прямоугольном треугольнике.

Синус угла можно найти, разделив длину противолежащего катета на гипотенузу:

sin(угол) = противолежащий катет / гипотенуза

Косинус угла можно найти, разделив длину прилежащего катета на гипотенузу:

cos(угол) = прилежащий катет / гипотенуза

Зная значения синуса и косинуса, можно перейти к нахождению гипотенузы.

Шаг 2: Используем формулу для определения гипотенузы

После того, как мы нашли значения синуса и косинуса для данного угла, мы можем использовать их, чтобы определить длину гипотенузы треугольника.

Формула для определения гипотенузы треугольника с использованием синуса и косинуса выглядит следующим образом:

гипотенуза = синус(угол) / косинус(угол)

Для примера, пусть у нас есть треугольник ABC, где угол B равен 45 градусов. Мы уже определили, что синус угла B равен 0.7071, а косинус угла B равен 0.7071. Теперь мы можем использовать эти значения в формуле:

гипотенуза = 0.7071 / 0.7071 = 1

Таким образом, в данном примере длина гипотенузы треугольника ABC равна 1.

Пример 1: Расчет гипотенузы треугольника с известными значениями синуса и косинуса

Предположим, что в треугольнике у нас известны значения синуса и косинуса угла между гипотенузой и катетом. Чтобы найти длину гипотенузы треугольника, следуйте следующим шагам:

1. Найдите значение синуса и косинуса угла между гипотенузой и катетом.
2. Используя формулу sin²(𝑥) + cos²(𝑥) = 1, проверьте, являются ли значения синуса и косинуса верными.
3. Рассчитайте значение гипотенузы, используя формулы 𝑠𝑖𝑛(𝑥) = 𝑜𝑝𝑝 / ℎ и 𝑐𝑜𝑠(𝑥) = 𝑎𝑑𝑗 / ℎ, где 𝑜𝑝𝑝 - длина катета, 𝑎𝑑𝑗 - длина гипотенузы, и ℎ - длина гипотенузы.

Давайте рассмотрим пример:

Допустим, у нас есть треугольник со синусом угла 60 градусов и косинусом угла 30 градусов. Чтобы найти длину гипотенузы, мы используем следующие шаги:

1. Задано: sin(60°) = 0.866 и cos(30°) = 0.866.
2. Проверяем, являются ли значения верными:

sin²(60°) + cos²(30°) = 0.866² + 0.866² ≈ 1

3. Рассчитываем значение гипотенузы:

sin(60°) = 𝑜𝑝𝑝 / ℎ → 0.866 = 𝑜𝑝𝑝 / ℎ

cos(30°) = 𝑎𝑑𝑗 / ℎ → 0.866 = 𝑎𝑑𝑗 / ℎ

Очевидно, что sin(60°) и cos(30°) равны между собой, поэтому мы можем предположить, что 𝑜𝑝𝑝 и 𝑎𝑑𝑗 равны между собой. Таким образом:

𝑜𝑝𝑝 = 𝑎𝑑𝑗 → 𝑎𝑑𝑗 = ℎ

А значит, длина гипотенузы равна 0.866 или приближенно 0.87.

Пример 2: Расчет гипотенузы через синус и косинус при известных значениях других сторон треугольника

Предположим, что у нас имеется прямоугольный треугольник ABC, где сторона AB (противолежащая прямому углу) равна 5 см, а сторона BC (прилежащая прямому углу) равна 3 см. Нам нужно найти длину гипотенузы AC.

Шаг 1: Пользуясь теоремой Пифагора, найдем квадрат длины гипотенузы AC:

AC^2 = AB^2 + BC^2

AC^2 = 5^2 + 3^2

AC^2 = 25 + 9

AC^2 = 34

Шаг 2: Для определения значения гипотенузы AC возьмем квадратный корень из полученного результата:

AC = √34 cm

Таким образом, при известных значениях других сторон треугольника, гипотенузу AC можно найти используя синус, косинус и теорему Пифагора. В данном примере гипотенуза AC равна примерно 5.83 см.