Наверняка каждый из нас помнит теорему Пифагора, которую мы учили в школе. Сегодня мы разберем, как ее использовать для нахождения длины гипотенузы по заданным катетам в треугольнике. Это очень полезное знание, особенно если вы занимаетесь геометрией, строительством или любым другим видом работы, связанным с треугольниками.
Для начала, давайте вспомним, что такое катеты и гипотенуза в треугольнике. Катетами называются две стороны треугольника, которые пересекаются в прямом угле. Гипотенуза - это самая длинная сторона треугольника, которая расположена напротив прямого угла. Зная значения катетов в треугольнике, мы можем использовать теорему Пифагора для нахождения длины гипотенузы.
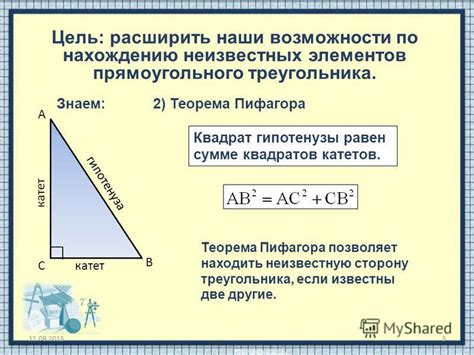
Теорема Пифагора утверждает, что квадрат длины гипотенузы равен сумме квадратов длин катетов. Математически это можно записать следующим образом: c^2 = a^2 + b^2, где c - длина гипотенузы, а и b - длины катетов.
Давайте рассмотрим пример, чтобы увидеть, как это работает. Предположим, у нас есть треугольник со сторонами a = 5 и b = 12. Чтобы найти длину гипотенузы, мы можем воспользоваться теоремой Пифагора: c^2 = 5^2 + 12^2 = 25 + 144 = 169. Чтобы найти длину гипотенузы, мы ищем квадратный корень из полученного числа: c = √169 = 13.
Что такое гипотенуза
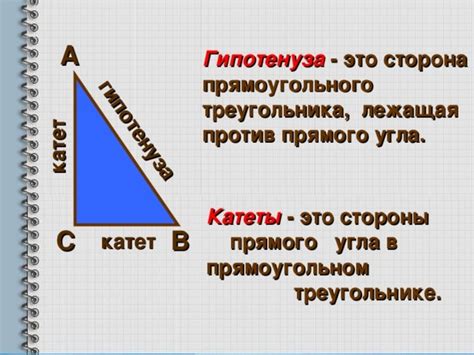
Гипотенуза обозначается буквой c и является основой для вычисления других параметров треугольника. Вычисление гипотенузы по катетам основано на применении теоремы Пифагора, которая устанавливает, что квадрат гипотенузы равен сумме квадратов катетов.
Зная длины двух катетов, можно использовать данную теорему для нахождения длины гипотенузы. Это может быть полезно для решения задач в геометрии, а также в практических областях, таких как строительство, физика и инженерия.
Определение гипотенузы
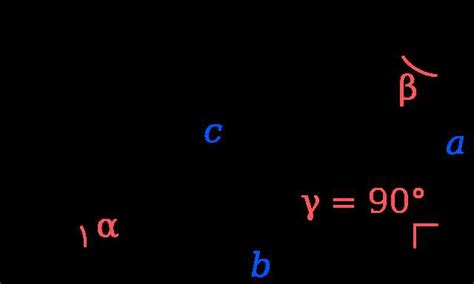
Для определения гипотенузы по катетам используется теорема Пифагора, которая гласит:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
То есть, если нам известны значения катетов a и b, мы можем определить значение гипотенузы c по формуле:
c = √(a^2 + b^2)
Метод нахождения гипотенузы по катетам занимает всего несколько шагов и может быть использован для решения множества задач, связанных с прямоугольными треугольниками.
Как найти гипотенузу по катетам
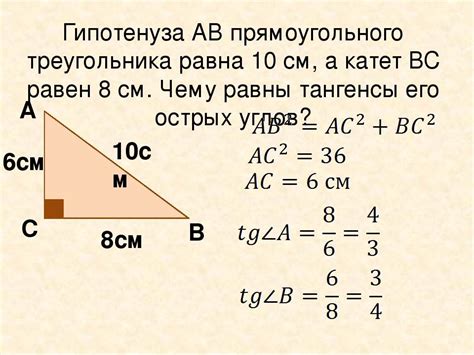
Теорема Пифагора утверждает, что квадрат длины гипотенузы равен сумме квадратов длин катетов. Формула записывается следующим образом:
c^2 = a^2 + b^2
где c - гипотенуза, а и b - катеты.
Поэтапно, чтобы найти гипотенузу по катетам, выполните следующие действия:
- Измерьте длины обоих катетов треугольника.
- Возведите в квадрат каждую из этих длин.
- Сложите полученные квадраты.
- Извлеките квадратный корень из полученной суммы.
Рассмотрим пример:
Допустим, что один катет треугольника равен 3 см, а другой - 4 см. Чтобы найти гипотенузу треугольника, используя теорему Пифагора, выполним следующие действия:
- Возведем 3 в квадрат: 3^2 = 9.
- Возведем 4 в квадрат: 4^2 = 16.
- Сложим полученные квадраты: 9 + 16 = 25.
- Извлекаем квадратный корень из полученного значения: √25 = 5.
Таким образом, гипотенуза треугольника равна 5 см.
Формула нахождения гипотенузы
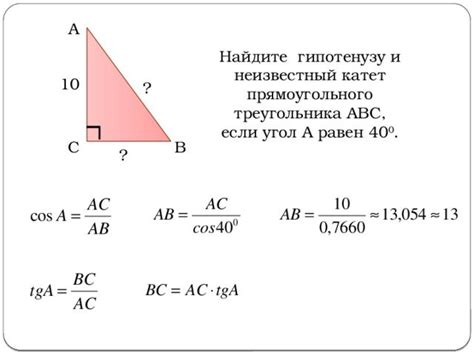
Формула нахождения гипотенузы:
- Если известны значения обоих катетов, то гипотенузу можно вычислить по формуле: гипотенуза = √(катет₁² + катет₂²).
- Если известна длина одного катета и гипотенузы, то можно воспользоваться следующей формулой: катет² = гипотенуза² - другой катет².
- Если известна длина одного катета и требуется найти длину гипотенузы, то можно использовать формулу: гипотенуза = √(катет² + гипотенуза²).
Формула нахождения гипотенузы является одной из базовых в геометрии и находит широкое применение в различных областях науки и повседневной жизни.
Шаги по нахождению гипотенузы
Для нахождения гипотенузы по катетам необходимо выполнить следующие шаги:
1. Определите значения двух катетов. Катеты - это две стороны прямоугольного треугольника, пересекающиеся в прямом углу.
2. Возведите каждый катет в квадрат, чтобы получить их квадраты.
3. Сложите полученные квадраты катетов.
4. Просуммируйте квадраты катетов.
5. Используя формулу Пифагора, возьмите квадратный корень из суммы квадратов катетов. Это будет гипотенуза.
6. Округлите полученное значение гипотенузы до необходимого количества знаков после запятой, если это требуется.
Теперь вы знаете, как найти гипотенузу по катетам прямоугольного треугольника. При использовании этих шагов вы сможете легко решать задачи, связанные с нахождением гипотенузы.
Шаг 1

Обозначим катеты как a и b. Подготовьте данные, которые у вас есть по этим катетам. Убедитесь, что вы знаете длину каждого катета.
Если величина катетов уже известна, переходите к следующему шагу, чтобы найти гипотенузу.
Шаг 2
После того как вы определили длины катетов, вам необходимо возвести их в квадрат. Для этого умножьте длину первого катета на самого себя (катет1*катет1) и получите значение первого квадрата.
Затем, умножьте длину второго катета на самого себя (катет2*катет2) и получите значение второго квадрата.
Следующий шаг - сложить эти два значения: первый квадрат и второй квадрат. Полученная сумма является квадратом гипотенузы.
Таким образом, для нахождения гипотенузы, вам нужно извлечь квадратный корень из полученной суммы.
Шаг 3

Сложите квадраты катетов. Вернитесь к предыдущим результатам и сложите полученные значения. Продолжая пример выше, сумма квадратов катетов будет равна 9 + 16 = 25.
Вычислите квадратный корень из суммы. Самое интересное на этом этапе: возьмите корень квадратный из значения, полученного на предыдущем шаге. В нашем примере, квадратный корень из 25 равен 5.
Поздравляю! Вы нашли гипотенузу! В нашем примере, гипотенуза равна 5. Ответ: гипотенуза = 5.
Примеры нахождения гипотенузы

Давайте рассмотрим несколько примеров, чтобы лучше понять, как найти гипотенузу по катетам.
Пример 1:
У нас есть прямоугольный треугольник со сторонами a = 4 и b = 3. Чтобы найти гипотенузу (позначим ее как c), мы используем теорему Пифагора:
c² = a² + b²
c² = 4² + 3²
c² = 16 + 9
c² = 25
c = √25
c = 5
Таким образом, гипотенуза треугольника равна 5.
Пример 2:
Предположим, что у нас есть треугольник со сторонами a = 7 и b = 24. Снова используем теорему Пифагора:
c² = a² + b²
c² = 7² + 24²
c² = 49 + 576
c² = 625
c = √625
c = 25
Гипотенуза этого треугольника равна 25.
Пример 3:
Предположим, что стороны треугольника a и b заданы как переменные. Например, a = 9 и b = 12.
Используя теорему Пифагора:
c² = a² + b²
c² = 9² + 12²
c² = 81 + 144
c² = 225
c = √225
c = 15
Таким образом, гипотенуза треугольника равна 15.