Гипотенуза – наибольшая сторона прямоугольного треугольника, соединяющая два катета. В геометрии, важно знать, как вычислить значение гипотенузы, особенно когда известны катет и косинус угла. Зная формулы и принципы, вы трансформируете прямоугольный треугольник во что-то большее, что поможет вам в решении более сложных задач.
Как найти гипотенузу по катету и косинусу угла? Есть несколько способов вычисления гипотенузы. Первый способ состоит в использовании формулы косинуса:
c = a / cos(β)
где c - гипотенуза, a - катет, а β - угол между гипотенузой и данной стороной треугольника.
Другой способ заключается в применении теоремы Пифагора:
c = √(a² + b²)
где c - гипотенуза, a и b - катеты. Используя эти формулы и зная соответствующие значения, вы сможете без труда вычислить гипотенузу и расширить свои знания в геометрии.
Гипотенуза: определение и свойства
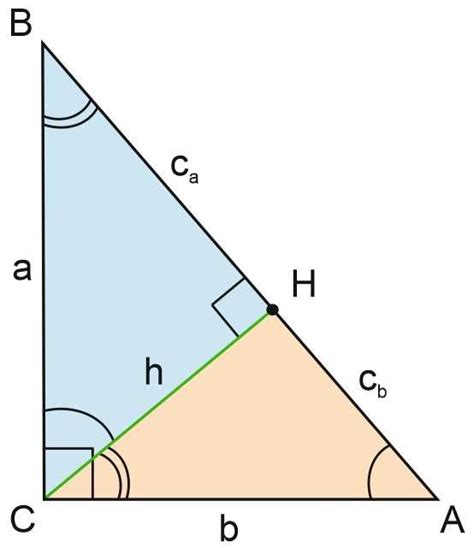
Гипотенуза обладает несколькими важными свойствами:
- Длина гипотенузы может быть вычислена с использованием формулы Пифагора: с^2 = a^2 + b^2, где a и b - длины катетов, а c - длина гипотенузы.
- Гипотенуза является основой для определения других свойств прямоугольного треугольника, таких как углы и площадь.
- Гипотенуза всегда больше каждого из катетов. Это следует из неравенства треугольника, которое утверждает, что сумма длин двух сторон треугольника всегда больше третьей стороны.
- Гипотенуза разделяет прямоугольный треугольник на два подобных треугольника с пропорциональными сторонами.
Знание свойств гипотенузы является важным для решения задач по нахождению ее длины и для общего понимания прямоугольных треугольников в математике и геометрии.
Формула нахождения гипотенузы по катету и косинусу угла
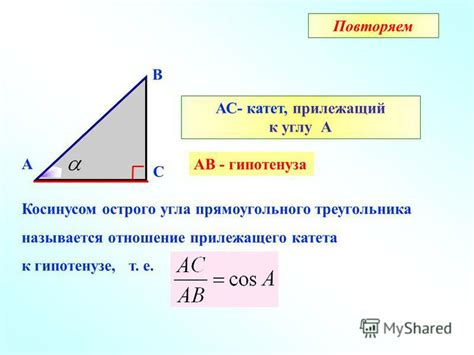
Для нахождения гипотенузы треугольника по известному катету и значению косинуса угла между гипотенузой и этим катетом можно использовать следующую формулу:
Гипотенуза = Катет / Косинус угла
Где:
- Гипотенуза - длина гипотенузы треугольника
- Катет - длина известного катета
- Косинус угла - значение косинуса угла между гипотенузой и катетом
Эта формула основана на определении косинуса угла как отношения длины катета к длине гипотенузы. Переписывая формулу, можно легко выразить длину гипотенузы.
Пример использования формулы:
Известно, что один катет треугольника равен 5 единицам длины, а косинус угла между гипотенузой и этим катетом составляет 0.8. Подставляя значения в формулу, получаем:
Гипотенуза = 5 / 0.8 = 6.25
Таким образом, длина гипотенузы треугольника равна 6.25 единицам.
Пример нахождения гипотенузы по катету и косинусу угла
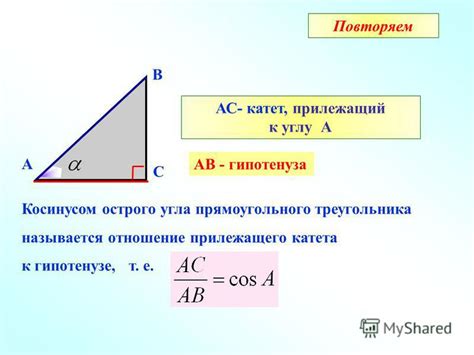
Допустим, у нас имеется прямоугольный треугольник, в котором известны длина катета a и значение косинуса угла между гипотенузой и катетом b. Нам нужно найти длину гипотенузы c.
Для этого мы можем использовать формулу:
c = a / cos(b)
Теперь рассмотрим пример:
Пусть у нас есть прямоугольный треугольник ABC, в котором катет AB равен 5 единицам длины, а косинус угла BAC равен 0,8. Мы хотим найти длину гипотенузы AC.
Используя формулу, подставим известные значения:
AC = 5 / 0,8
AC = 6,25
Таким образом, длина гипотенузы AC равна 6,25 единицам длины.
Значение гипотенузы в различных задачах
1. Нахождение гипотенузы по катетам. Если известны значения двух катетов a и b в прямоугольном треугольнике, то можно найти гипотенузу с помощью теоремы Пифагора: c = √(a² + b²), где c - гипотенуза.
2. Нахождение гипотенузы по одному катету и косинусу угла. Если известен катет a и косинус угла α между гипотенузой и этим катетом, то можно использовать формулу: с = a/cos(α), где c - гипотенуза.
3. Применение гипотенузы в задачах на расстояние и скорость. В физике гипотенуза может быть использована для определения расстояния, пройденного телом со скоростью v за время t: s = v*t = c, где s - расстояние, v - скорость, t - время, c - гипотенуза.
4. Применение гипотенузы в задачах на оптику. В оптике гипотенуза может использоваться для определения пути светового луча после отражения или преломления при использовании законов лучевой оптики.
5. Применение гипотенузы в задачах на механику. В механике гипотенуза может использоваться для определения силы трения, применяемой к телу при его движении по наклонной плоскости.
Использование знания о гипотенузе позволяет решать различные математические и физические задачи, связанные с геометрией, оптикой, тригонометрией и механикой.
Косинус угла: определение и свойства
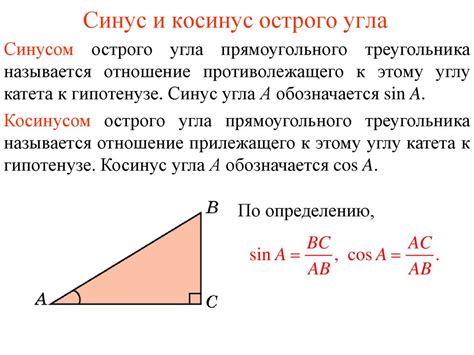
Свойства косинуса угла:
- Определение: Косинус угла определяется как отношение длины прилежащего катета к длине гипотенузы в прямоугольном треугольнике.
- Значение: Косинус угла может принимать значения от -1 до 1.
- Симметричность: Косинус угла имеет симметричность относительно оси ординат: cos(−θ) = cos(θ).
- Периодичность: Косинус угла имеет период равный 2π: cos(θ + 2π) = cos(θ).
- Основные значения: Некоторые основные значения косинуса угла: cos(0) = 1, cos(π/2) = 0, cos(π) = -1.
Косинус угла является одной из важных тригонометрических функций и позволяет решать различные задачи, связанные с прямоугольными треугольниками и углами, а также применяется во многих областях науки и техники.
Формула нахождения косинуса угла по катету и гипотенузе
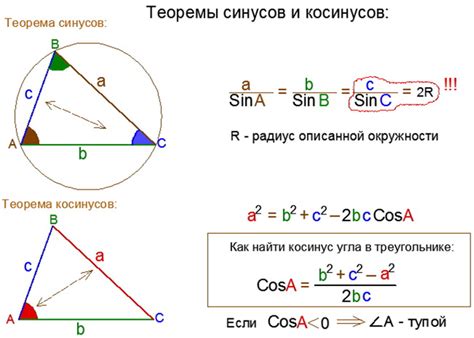
Для нахождения косинуса угла (cos α) по известным значениям катета (a) и гипотенузы (c) можно использовать формулу:
cos α = a/c
Найдя значение косинуса угла по этой формуле, можно далее использовать его для решения различных задач, например, для нахождения значения другого катета или угла в треугольнике.
Пример нахождения косинуса угла по катету и гипотенузе

Как известно, косинус угла можно вычислить по формуле:
cos(α) = катет / гипотенуза
Давайте рассмотрим конкретный пример:
У нас есть прямоугольный треугольник, в котором известны катет и гипотенуза. Катет равен 5, а гипотенуза равна 10.
Тогда, подставив значения в формулу, получим:
cos(α) = 5 / 10 = 0.5
Таким образом, косинус угла α равен 0.5.
Такой пример поможет лучше понять, как можно использовать формулу для нахождения косинуса угла по известным катету и гипотенузе.