Центральная окружность – это особый тип окружности, который имеет центр и радиус. Каждая точка на окружности находится на одинаковом расстоянии от центра. Одно из основных свойств центральной окружности – её градусная мера, которая помогает понять, насколько она "раскрывается" на плоскости.

Для того чтобы найти градусную меру центральной окружности, необходимо знать её радиус и длину дуги. Это позволит нам использовать простую формулу для вычисления угла. Также, можно использовать и другие величины вместо длины дуги – длину хорды или площадь сектора.

Один градус – это 1/360 часть полного оборота. Поэтому градусную меру центральной окружности можно найти, разделив длину дуги на длину окружности и умножив на 360.

Определение градусной меры центральной окружности

Для определения градусной меры центральной окружности используется понятие дуги окружности. Дуга окружности – это часть окружности, которая ограничена двумя точками на окружности. Градусная мера дуги определяется с помощью угла, образуемого дугой и центром окружности.

Если положить, что градусная мера полной окружности равна 360 градусов, то градусная мера любой дуги окружности будет определяться по формуле, где x – градусная мера дуги, L – длина дуги, а R – радиус окружности.

Градусная мера центральной окружности имеет важное значение при решении задач геометрии и математики, а также в приложениях в физике и других науках.

Формула расчета градусной меры центральной окружности

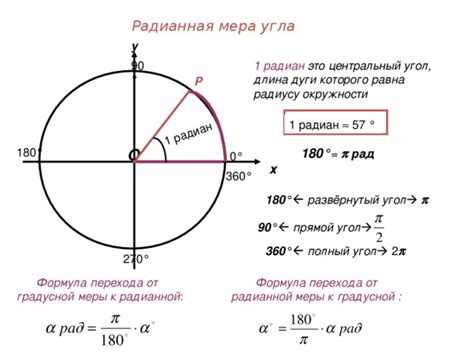
Для расчета градусной меры центральной окружности необходимо учесть величину угла, который образует данный сектор окружности.

Формула для расчета градусной меры центральной окружности выглядит следующим образом:

Градусная мера центральной окружности = Длина дуги / Радиус окружности * 360

В данной формуле длина дуги измеряется в единицах длины, радиус окружности - в тех же единицах, а градусная мера выражается в градусах.

Таким образом, зная длину дуги и радиус окружности, можно легко вычислить градусную меру центральной окружности.

Значение градусной меры центральной окружности в геометрии

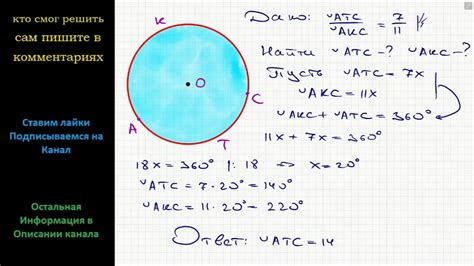
Углы, образованные на окружности, измеряются в градусах. Градусная мера окружности равна 360 градусам. Однако, важно отметить, что центральная окружность может быть разделена на более мелкие дуги, которые также имеют градусную меру.

Для нахождения градусной меры центральной окружности необходимо знать длину дуги, выраженную в градусах. Формула для нахождения градусной меры дуги на окружности имеет вид:

l = (d / r) * 180° / π

где l - градусная мера дуги, d - длина дуги, r - радиус окружности, π - число пи (приближенно равно 3.14).

Таким образом, зная длину дуги и радиус окружности, мы можем вычислить градусную меру центральной окружности.

Градусная мера центральной окружности имеет важное значение в геометрии и помогает в решении различных задач, связанных с окружностями и углами. Понимание этого концепта позволяет проводить геометрические вычисления и использовать их в практических задачах.