Градусная мера угла в окружности является одним из ключевых понятий геометрии, изучаемых восьмиклассниками. Научиться находить градусную меру угла поможет легко и точно определять его положение и величину на окружности. Для этого необходимо ознакомиться с основными правилами и формулами, которые мы рассмотрим в данной статье.
Перед изучением нахождения градусной меры угла в окружности необходимо понимать, что окружность делится на 360 градусов. Каждый градус равен 1/360 от общей длины окружности. Это важное представление позволяет нам легко определить градусную меру угла в окружности и использовать её в решении различных геометрических задач.
Чтобы найти градусную меру угла в окружности, необходимо знать длину дуги, которую он охватывает. Градусная мера угла можно определить с использованием пропорции:
Градусная мера угла = (длина дуги / длина окружности) * 360 градусов.
Теперь, имея основные знания и формулы, мы можем эффективно находить градусную меру угла в окружности. Эти навыки будут полезны в решении разнообразных задач и в дальнейшем изучении геометрии.
Определение градусной меры угла

Для определения градусной меры угла необходимо знать соотношение между углом и длиной дуги, которую он заключает на окружности. Полный оборот окружности составляет 360°, что означает, что при повороте на 360° точка возвращается в исходное положение.
Градусы делятся на минуты и секунды. 1 градус содержит 60 минут, а 1 минута содержит 60 секунд. Символы для обозначения минут и секунд – ‘ и ’ соответственно.
Для измерения углов применяют различные инструменты, такие как транспортир, гониометр и специальные приборы для измерения углов на радианы.
Измерение градусной меры угла имеет множество практических применений. Например, в картографии, в навигации, в физике и во многих других областях, где изучаются и анализируются углы в пространстве.
Основные понятия
Диаметр окружности - отрезок, соединяющий две точки на окружности и проходящий через ее центр.
Радиус окружности - половина диаметра. Обозначается буквой "r".
Центральный угол - угол с вершиной в центре окружности, его сторонами являются лучи, исходящие из центра и проходящие через две точки на окружности.
Градусная мера угла - величина, измеряемая в градусах, указывающая, насколько одно измерение вращения имеет преимущество перед другим вращением в той же плоскости.
Полный угол - угол, равный 360 градусам, соответствует одному обороту вокруг центра окружности.
Дуга - часть окружности, ограниченная двумя точками.
Линейка - измерительная шкала, используемая для измерения длины отрезков или дуг на окружности. Обозначается буквой "L".
Длина окружности - сумма длин всех дуг на окружности. Обозначается буквой "C".
Соотношение длины окружности к ее радиусу: C = 2 * П * r.
Окружность и ее элементы
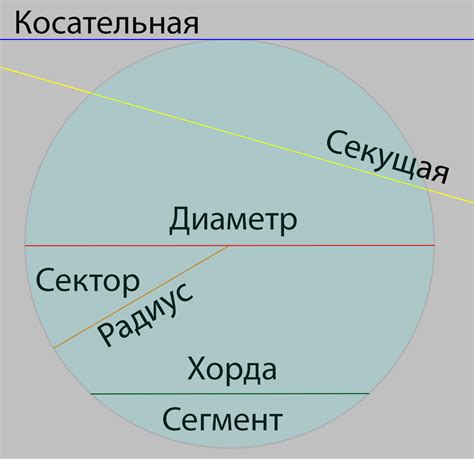
Диаметр - это отрезок, проходящий через центр окружности и соединяющий две точки на окружности. Диаметр делит окружность на две равные части, называемые полуокружностями.
Радиус - это отрезок, соединяющий центр окружности с любой точкой на окружности. Радиус является половиной диаметра и обозначается символом "r".
Длина окружности - это общая длина всех сегментов окружности. Длину окружности можно вычислить, используя формулу: L = 2πr, где "L" - длина окружности, "π" - математическая константа, равная примерно 3,14, и "r" - радиус окружности.
Угол в окружности - это угол между двумя лучами, исходящими из центра окружности и проходящими через две точки на окружности. Полный угол в окружности равен 360°, а половина - 180°. Любой угол в окружности можно измерить в градусах.
Градусная мера угла в окружности связана с длиной дуги окружности и радиусом. Для нахождения градусной меры угла можно использовать формулу: α = (l / L) * 360°, где "α" - градусная мера угла, "l" - длина дуги окружности, "L" - длина окружности.
Угол на окружности
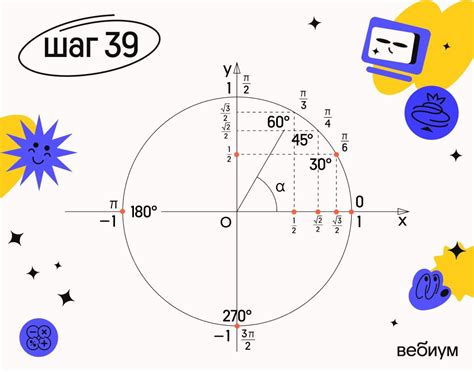
Для нахождения градусной меры угла на окружности требуется знать длину дуги, определяемой этим углом, и её соотношение с полной окружностью.
Строится пропорция, в которой градусная мера угла обозначается символом α, длина дуги - L, а полная окружность - С:
| α (градусы) | : | L (длина дуги) |
| 360 (градусов) | : | C (полная окружность) |
Исходя из этой пропорции, можно найти градусную меру угла на окружности:
α = (L × 360) / C
Таким образом, для нахождения градусной меры угла на окружности необходимо знать длину дуги и полную окружность.
Формула для нахождения градусной меры угла

Угол в окружности измеряется в градусах. Чтобы найти градусную меру угла, нужно знать его длину в радианах и использовать формулу:
| Градусная мера угла | = | (Длина угла в радианах × 180) ÷ π |
В этой формуле "Длина угла в радианах" - это длина угла, измеренная в радианах. Значение π (пи) равно примерно 3.14159.
Давайте рассмотрим пример: если длина угла в радианах равна 2π, то для нахождения градусной меры угла мы подставим это значение в формулу:
| Градусная мера угла | = | (2π × 180) ÷ π | |
| = | 2 × 180 | = | 360 градусов |
Таким образом, угол длиной 2π радиана равен 360 градусам.
Используя эту формулу, вы сможете легко находить градусные меры углов в окружности.
Теорема о центральном угле
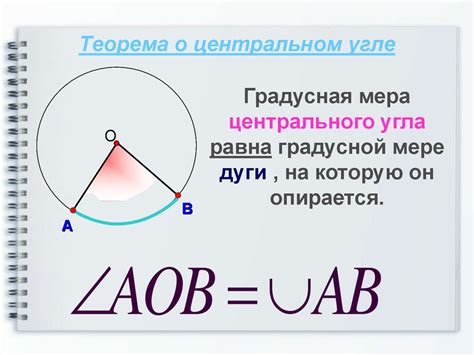
Согласно теореме о центральном угле, градусная мера центрального угла в окружности равна мере дуги, соответствующей этому углу. То есть, если дуга на окружности охватывает угол в 60 градусов, то и сам угол равен 60 градусам. При этом полный центральный угол в окружности равен 360 градусам, так как полная окружность состоит из 360 градусов.
Для вычисления градусной меры центрального угла в окружности можно использовать такую формулу:
| Угол | Мера дуги |
|---|---|
| α | α |
| β | β |
| γ | γ |
| δ | δ |
Где α, β, γ и δ – градусные меры данных углов, а их меры дуг соответственно такие же.
Теорема о центральном угле позволяет решать множество задач, связанных с измерением углов в окружностях, а также является важной основой для дальнейшего изучения геометрии и тригонометрии.
Правило нахождения градусной меры угла
Градусная мера угла в окружности может быть найдена по следующему правилу:
Если в окружности есть центральный угол, который содержит n радиан, то градусная мера этого угла равна 180n/π градусов.
Таким образом, чтобы найти градусную меру угла, нужно знать его радианную меру и воспользоваться данным правилом.