Изучение геометрии - неотъемлемая часть любого математического курса. Одно из ключевых понятий, с которым сталкиваются ученики в школе - это окружность и углы, которые в ней содержатся. Понимание градусной меры угла в окружности является основой для дальнейшего изучения геометрических фигур и их свойств.

Если вам нужно найти градусную меру угла в окружности известного угла, то это можно сделать с помощью специальной формулы. В основе формулы лежит основное свойство окружности, которое гласит, что сумма всех углов в окружности равняется 360 градусов. Таким образом, если вам известна градусная мера одного из углов в окружности, то остальные углы можно выразить с помощью этой формулы.

Представим, что у нас есть угол, градусная мера которого известна. Обозначим эту меру как "x". Остальные углы в окружности можно выразить следующим образом: если "x" - это градусная мера одного из углов, то остальные углы можно выразить как 360 - "x". Таким образом, если известна мера угла "x", то градусная мера другого угла будет равна 360 - "x".

Разбираясь с градусной мерой угла в окружности, важно помнить, что сумма всех углов в окружности равняется 360 градусов. Используя специальные формулы и знание основных свойств окружности, вы сможете находить градусные меры углов в окружности, имея информацию о градусной мере одного из них.

Определение градусной меры угла в окружности

Для определения градусной меры угла в окружности используется формула, основанная на соотношении между длиной дуги и радиусом окружности. Если известна длина дуги, то градусная мера угла может быть найдена следующим образом:

Градусная мера угла = (Длина дуги / Длина окружности) * 360°

Здесь Длина дуги - это фактическая длина угла, измеряемая в единицах длины, например, сантиметрах или метрах. Длина окружности - это общая длина окружности и может быть вычислена по формуле 2πr, где r - радиус окружности.

Используя данную формулу, можно определить градусную меру угла в окружности, если известны его длина и радиус окружности. Это полезное знание при работе с геометрическими задачами, расчетами и измерениями вокруг окружностей.

Углы в окружности и их градусная мера:

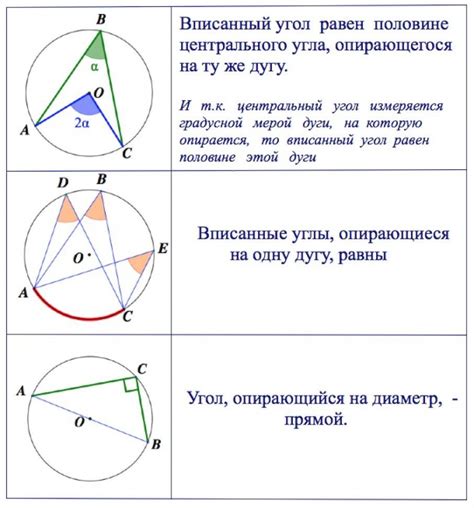
Градусная мера угла в окружности определяется длиной дуги, которую он охватывает. Если угол охватывает всю окружность, его градусная мера равна 360 градусов. Если угол охватывает половину окружности, его градусная мера равна 180 градусов.

Формула для нахождения градусной меры угла в окружности:

градусная мера = (длина дуги / длина окружности) * 360

Для нахождения градусной меры угла в окружности нужно знать длину дуги, которую он охватывает, и длину окружности, в которую вписана эта дуга.

Расчет градусной меры угла в окружности:

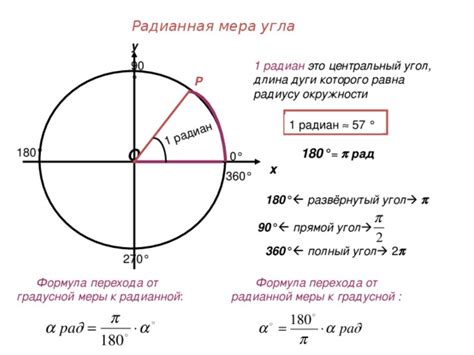
Для расчета градусной меры угла в окружности мы можем использовать знание о том, что в окружности 360 градусов. Это означает, что если известна доля угла относительно полного оборота, мы можем найти его градусную меру.

Формула для расчета градусной меры угла в окружности выглядит следующим образом:

Градусная мера угла = (Доля угла/полный оборот) * 360

Например, если известно, что угол составляет 1/4 от полного оборота, то его градусная мера будет:

Градусная мера угла = (1/4) * 360 = 90 градусов

Таким образом, при помощи указанной формулы мы можем легко рассчитать градусную меру угла в окружности, зная его долю относительно полного оборота.

Примеры использования:

1. Если угол составляет 1/8 от полного оборота:

Градусная мера угла = (1/8) * 360 = 45 градусов

2. Если угол составляет 3/4 от полного оборота:

Градусная мера угла = (3/4) * 360 = 270 градусов

Пример решения задачи:

Пусть у нас есть угол, измеренный в радианах, равный 2.5.

Чтобы найти градусную меру этого угла, нужно воспользоваться формулой: градусная мера = (угол в радианах * 180) / Пи.

Подставив значения, получим: градусная мера = (2.5 * 180) / Пи.

Вычислив это выражение, получим около 142.7 градусов.

Таким образом, угол в радианах, равный 2.5, соответствует примерно 142.7 градусам.

Итоги:

При решении задачи по нахождению градусной меры угла в окружности известного угла необходимо использовать формулу:

{{ формула }}

где {{ фраза }}.

В данной статье мы рассмотрели основные шаги для нахождения градусной меры угла в окружности известного угла. Сначала мы проанализировали задачу и построили рисунок, чтобы лучше понять ситуацию. Затем мы воспользовались геометрическими свойствами окружностей и углами, чтобы вывести формулу для нахождения искомой величины.

Для решения этой задачи необходимо учесть различные варианты расположения угла относительно окружности и выбрать соответствующую формулу. Важно также обратить внимание на единицы измерения, которые мы используем (градусы или радианы). Кроме того, нужно быть внимательным при подстановке значений в формулу, чтобы не допустить ошибки в вычислениях.

В результате наших вычислений мы определили градусную меру угла в окружности известного угла и получили ответ: {{ ответ }}.