Прямоугольный треугольник – это треугольник, в котором один из углов равен 90 градусам. Он имеет два катета и гипотенузу. Катеты - это две стороны, которые образуют прямой угол, а гипотенуза - это самая длинная сторона треугольника. Возникает вопрос: как найти длину одного из катетов? На помощь приходят геометрические формулы и знание тригонометрии.
Формула для нахождения катета прямоугольного треугольника основывается на теореме Пифагора:
Катет = квадрат гипотенузы минус квадрат другого катета
Найдя длину одного катета можно найти длину второго катета, так как они равны друг другу. Это позволяет нам определить все стороны треугольника.
Есть и другой способ нахождения катета прямоугольного треугольника. Он основывается на тригонометрических функциях, а точнее, на соотношениях синуса и косинуса. Если известна гипотенуза и один из углов треугольника, то можно найти значение катета с помощью тригонометрических функций.
Катет прямоугольного треугольника: формула и через угол
Формула:
Для нахождения катета прямоугольного треугольника можно использовать теорему Пифагора. Она гласит, что квадрат длины гипотенузы равен сумме квадратов длин катетов.
Формула для нахождения длины катета выглядит следующим образом:
c^2 = a^2 + b^2
где c - гипотенуза, a и b - катеты.
Нахождение катета через угол:
Второй способ нахождения катета основан на использовании известного угла. Если известны угол и длина гипотенузы, можно вычислить длину одного из катетов с помощью тригонометрических функций - синуса, косинуса или тангенса.
Для нахождения катета по углу можно использовать следующие формулы:
Синус: a = c * sin(α)
Косинус: a = c * cos(α)
Тангенс: a = c * tan(α)
где a - катет, c - гипотенуза, α - угол между гипотенузой и катетом.
Используя эти формулы, вы сможете вычислить длину катета прямоугольного треугольника как по теореме Пифагора, так и через известный угол.
Нахождение катета через второй катет и гипотенузу
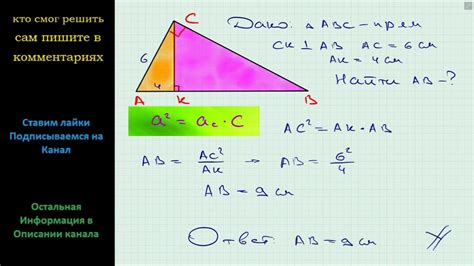
Для нахождения катета прямоугольного треугольника через известные значения второго катета и гипотенузы, мы можем использовать теорему Пифагора. Теорема Пифагора утверждает, что квадрат гипотенузы равен сумме квадратов катетов.
Пусть a и c - соответственно второй катет и гипотенуза треугольника. Тогда согласно теореме Пифагора:
a2 = c2 - b2
Где a - катет, c - гипотенуза, b - второй катет.
Для нахождения катета a, нужно знать значения гипотенузы c и второго катета b. Подставляя известные значения в формулу, можно рассчитать искомый катет.
Пример:
Пусть второй катет треугольника равен 3, а гипотенуза равна 5. Тогда, подставляя значения b=3 и c=5 в формулу, получаем:
a2 = 52 - 32 = 25 - 9 = 16
a = √16 = 4
Таким образом, искомый катет равен 4.
Нахождение катета через угол и гипотенузу
Для нахождения катета прямоугольного треугольника с помощью угла и гипотенузы можно использовать формулу синуса:
- Установите значение гипотенузы (стороны, противолежащей прямому углу) и угла, заданного в радианах;
- Используя формулу синуса, для нахождения катета примените следующую формулу: катет = гипотенуза * sin(угол).
Примером может быть ситуация, когда угол равен 30 градусам, а гипотенуза имеет длину 10 единиц. Для нахождения катета воспользуемся формулой:
катет = 10 * sin(30°) = 10 * 0.5 = 5 единиц.
Теперь, имея гипотенузу и значение угла, вы сможете использовать формулу синуса, чтобы найти длину нужного вам катета. Помните, что все углы должны быть заданы в радианах.
Практическое использование формулы для нахождения катета

Формула для нахождения катета прямоугольного треугольника может быть очень полезна в различных практических ситуациях. Она позволяет определить длину катета, если известны другой катет и гипотенуза треугольника.
Применение данной формулы особенно полезно, например, при строительстве дома или выполнении других строительных работ, когда необходимо определить длину стороны треугольника на основе известных данных. Также она может быть использована в приложениях геометрии, физики и других научных дисциплинах.
Помимо формулы, катет можно также найти через угол. Для этого необходимо знать длину гипотенузы и значение угла между гипотенузой и искомым катетом. В этом случае применяются тригонометрические функции, такие как синус, косинус или тангенс.
Практическое использование формулы для нахождения катета требует правильного применения формул и учета известных данных. Разумное использование этой формулы позволяет решать разнообразные задачи и облегчает работы, где необходимо знать длину катета прямоугольного треугольника.
Расчет катета в прямоугольном треугольнике: примеры и задачи
Формула для нахождения катета в прямоугольном треугольнике:
Если известны длины гипотенузы (c) и другого катета (a), можно использовать теорему Пифагора, чтобы найти длину второго катета (b):
b = √(c^2 - a^2)
Задача:
Пусть в прямоугольном треугольнике длина гипотенузы (c) равна 10, а длина одного катета (a) равна 6. Найдем длину второго катета (b) по формуле:
| c | a | b |
|---|---|---|
| 10 | 6 | √(10^2 - 6^2) |
| √(100 - 36) | ||
| √64 | ||
| 8 |
Таким образом, длина второго катета (b) в прямоугольном треугольнике равна 8.
Это был пример расчета катета в прямоугольном треугольнике с использованием формулы и известных данных. Зная значения гипотенузы и другого катета, можно решать подобные задачи и находить длину нужного катета. Также, существуют другие методы расчета катетов, например, через известный угол треугольника. Они более сложные и требуют знания тригонометрии.