Прямоугольный треугольник – одна из основных фигур геометрии, которая имеет особые свойства и является основой для решения множества задач. Одной из таких задач является нахождение катетов прямоугольного треугольника по известной гипотенузе. Это может быть полезно в различных сферах, от строительства до астрономии.
Для решения задачи необходимо использовать теорему Пифагора, которая гласит: сумма квадратов катетов равна квадрату гипотенузы. Поэтому, если известна длина гипотенузы, можно найти длины катетов с помощью математических операций: извлечение квадратного корня и возведение в квадрат.
Ниже приведена схема решения задачи. Пусть a и b – катеты прямоугольного треугольника, а c – гипотенуза. В соответствии с теоремой Пифагора, справедливо уравнение: a^2 + b^2 = c^2. Если известна длина гипотенузы c, катеты a и b могут быть найдены с помощью следующих выражений:
a = √(c^2 - b^2)
b = √(c^2 - a^2)
Используя эти выражения, можно найти значения катетов прямоугольного треугольника по известной длине гипотенузы. Такое решение позволяет решать задачи в различных областях и применениях, где требуется нахождение значений катетов.
Поиск катетов прямоугольного треугольника по гипотенузе:

В прямоугольном треугольнике существует связь между длинами его катетов и гипотенузы. Если известна длина гипотенузы и одного из катетов, можно найти второй катет, используя теорему Пифагора:
Теорема Пифагора: "В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы".
Используя эту теорему, можно выразить второй катет через известные значения:
c^2 = a^2 + b^2
Где:
- c - длина гипотенузы
- a - длина одного из катетов
- b - длина второго катета (который мы хотим найти)
Шаги для поиска второго катета по известным значениям:
- Возведите в квадрат известное значение гипотенузы.
- Возведите в квадрат известное значение первого катета.
- Из выражения c^2 = a^2 + b^2 вычтите квадрат первого катета из квадрата гипотенузы, чтобы найти квадрат второго катета.
- Извлеките квадратный корень из полученного значения, чтобы найти длину второго катета.
Поиск катетов прямоугольного треугольника по гипотенузе позволяет решать множество задач в геометрии, а также в различных областях науки и техники, где требуется работа с прямоугольными треугольниками.
Инструкция для вычисления катетов

Чтобы вычислить катеты прямоугольного треугольника по известной гипотенузе, следуйте следующей инструкции:
- Определите значение гипотенузы треугольника. Это сторона, противолежащая прямому углу и самая длинная сторона треугольника.
- Определите, какой катет вы хотите вычислить - примем его за первый катет.
- Используя теорему Пифагора, найдите значение второго катета. Формула для вычисления второго катета: второй катет = квадрат гипотенузы минус квадрат первого катета, все под корнем.
- Если требуется вычислить оба катета, повторите шаги 2-3 для второго катета.
Эта инструкция поможет вам вычислить значения катетов прямоугольного треугольника, если известна длина гипотенузы. Приложенная схема поможет вам визуализировать процесс вычисления.
Схема вычисления катетов
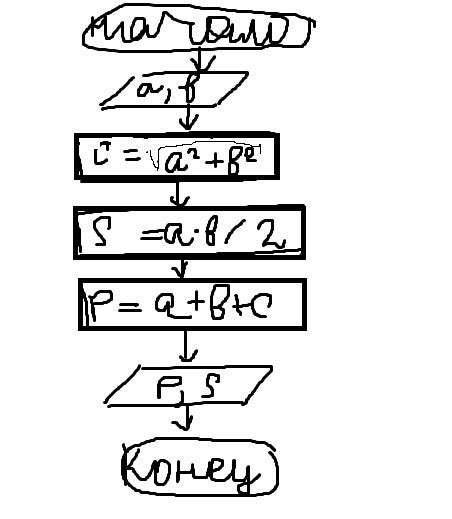
Вычисление катетов прямоугольного треугольника по известной гипотенузе может быть выполнено с использованием следующей схемы:
| Шаг 1: | Задать значение гипотенузы треугольника |
| Шаг 2: | Выбрать катет, который нужно найти |
| Шаг 3: | Используя теорему Пифагора, вычислить значение катета: |
катет = √(гипотенуза² - другой_катет²) | |
| Шаг 4: | Проверить полученное значение катета на соответствие допустимым значениям |
| Шаг 5: | Повторить шаги 2-4 для другого катета, если необходимо |
С помощью этой схемы можно быстро и точно найти значения катетов прямоугольного треугольника по известной гипотенузе. Данный подход особенно полезен при решении задач геометрии и в других областях, где требуется работать с прямоугольными треугольниками.