Треугольник является одной из основных геометрических фигур, которая имеет множество свойств и особенностей. Одной из важных составляющих треугольника является его сторона, из которых две называются катетами, а одна - гипотенузой. Как найти катеты треугольника, зная гипотенузу?
В этой статье мы рассмотрим основные методы решения данной задачи. Первый метод основан на использовании теоремы Пифагора. Согласно этой теореме, квадрат гипотенузы треугольника равен сумме квадратов катетов. Из этой формулы можно выразить один из катетов через гипотенузу и другой катет.
Еще один метод, который можно применить для нахождения катетов треугольника, - использование тригонометрических функций. Например, если известен угол между гипотенузой и одним из катетов, то для нахождения катета можно воспользоваться тангенсом этого угла. Для нахождения второго катета можно использовать косинус или синус угла.
Основные методы нахождения катетов треугольника, зная гипотенузу
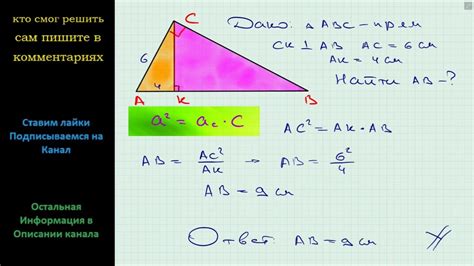
В геометрии существуют различные методы для нахождения катетов треугольника, если известна его гипотенуза. В данной статье мы рассмотрим несколько основных методов, которые помогут вам решить эту задачу.
Метод Пифагора
Метод Пифагора основывается на знаменитой теореме, которая гласит: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Для нахождения одного из катетов, зная гипотенузу, нужно вычесть из квадрата гипотенузы квадрат другого катета и извлечь квадратный корень из полученного значения.
Формула:
| Катет: | a = √(c^2 - b^2) |
| Катет: | b = √(c^2 - a^2) |
Метод подобных треугольников
Если треугольник прямоугольный, то его катеты пропорциональны соответствующим катетам другого прямоугольного треугольника. Это означает, что можно составить пропорции и решить их, чтобы найти значения катетов.
Формула:
| Катет: | a = (c * a1) / c1 |
| Катет: | b = (c * b1) / c1 |
Где c1 и c2 - известные катеты и c - известная гипотенуза, a1 и b1 - искомые катеты.
Выведенные выше методы являются основными и широко используются для нахождения катетов треугольника по известной гипотенузе. Надеемся, что они прояснили данную тему и помогут вам в решении задач с треугольниками.
Метод использования теоремы Пифагора

Для использования теоремы Пифагора в задачах по нахождению катетов треугольника, если известна гипотенуза, нужно следовать следующим этапам:
- Определить известные значения.
- Поставить условие задачи в виде уравнения.
- Воспользоваться теоремой Пифагора и заменить переменные на известные значения.
- Решить полученное уравнение, перенося все известные значения на одну сторону и оставив неизвестные на другой.
- Найти корень из получившегося значения, чтобы найти отсутствующий катет.
Например, если известна гипотенуза треугольника и один из катетов, то можно найти второй катет, применяя теорему Пифагора. Подставив известные значения в формулу и решив уравнение, можно найти длину отсутствующего катета треугольника.
Использование теоремы Пифагора является эффективным методом для нахождения катетов треугольника, так как он позволяет найти недостающее значение, если известны два других.