Квадратное уравнение – это одно из основных понятий алгебры, которое встречается в школьной программе. Оно имеет вид ax^2 + bx + c = 0, где a, b и c – это коэффициенты, а x – неизвестная переменная. Определение этих коэффициентов по графику квадратного уравнения является одним из методов решения задачи и позволяет получить более наглядную и практическую интерпретацию.
Как найти коэффициенты квадратного уравнения по графику? Для начала необходимо вспомнить основные свойства квадратных функций и графиков. График квадратной функции имеет форму параболы, которая может быть направленна вниз или вверх в зависимости от знака коэффициента a. Если парабола направлена вверх, то коэффициент a будет положительным, а если парабола направлена вниз, то коэффициент a будет отрицательным.
Зная, как расположена парабола на графике, можно определить остальные коэффициенты. Коэффициент c получается из точки пересечения параболы с осью ординат (ось y). Зная значение c, можно определить, где на графике проходит парабола относительно оси y. Коэффициент b определяется по координатам вершины параболы, которая лежит на оси x. Зная координаты вершины, можно найти значение b.
Поиск коэффициентов квадратного уравнения

Есть несколько способов найти коэффициенты квадратного уравнения, и один из них – использовать график функции, представляющей это уравнение.
Когда у вас есть график квадратного уравнения, вы можете определить значения коэффициентов, исходя из его характеристик.
| График | Коэффициенты |
|---|---|
| Отрезок оси абсцисс, на котором график пересекает ее | Коэффициент c |
| Отрицательный коэффициент a делает график дугой на верхней части и открывается внизу | Коэффициент a |
| Коэффициенты b и c влияют на положение вершины параболы | Коэффициенты b и c |
| Наклон графика | Не имеет прямой связи с коэффициентами |
Зная характеристики графика и связанные с ними коэффициенты, можно найти значения a, b и c квадратного уравнения.
Важно помнить, что данный способ не является единственным, и существуют и другие способы нахождения коэффициентов. Однако использование графика позволяет получить представление о форме квадратного уравнения и его коэффициентах без прямого аналитического решения.
Коэффициенты квадратного уравнения в графике
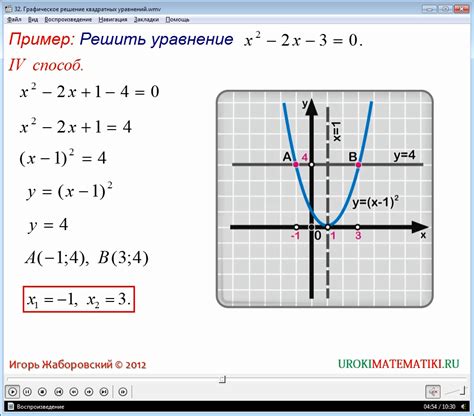
Первая ключевая точка - вершина графика. Самый простой способ найти координаты вершины - это использовать формулы: x = -b / (2a) и y = c - b^2 / (4a). Зная координаты вершины, а именно (x, y), можно найти значение коэффициента c.
Вторая ключевая точка - точка пересечения графика с осью ординат, также называемая корнем уравнения. Корни можно найти, приравняв y к нулю и решив уравнение: ax^2 + bx + c = 0. Найденные корни могут дать информацию о коэффициентах a и b.
Если график квадратного уравнения пересекает ось ординат в одной точке, то уравнение имеет один корень, и следовательно, a = 0, b = 0, и c = y. Если график пересекает ось ординат в двух точках, то можно использовать координаты обоих корней для нахождения a и b.
Примечание. Если график квадратного уравнения не пересекает ось ординат, то уравнение не имеет корней.
Пользуясь этими ключевыми точками, можно определить значения коэффициентов квадратного уравнения и построить его график. Это оказывается полезным при решении задач, моделировании и анализе квадратных уравнений.
Методы поиска коэффициентов квадратного уравнения

Существует несколько методов для поиска коэффициентов квадратного уравнения:
- Метод коэффициентов - данный метод основан на знании хотя бы трех точек, принадлежащих графику квадратного уравнения. Используя эти точки, можно сформулировать систему уравнений и решить ее, чтобы найти значения коэффициентов. Этот метод требует некоторых навыков работы с линейными уравнениями и системами уравнений.
- Метод разложения на множители - данный метод основан на осознании того, что квадратное уравнение может быть представлено как произведение двух линейных множителей. Если известно, что уравнение имеет корни, то можно воспользоваться этим методом, разложив уравнение на множители и определив значения коэффициентов. Для более сложных уравнений может потребоваться использование формулы Виета.
- Методы аппроксимации - если график квадратного уравнения не проходит через конкретные заданные точки, можно использовать методы аппроксимации для приближенного определения коэффициентов. Наиболее распространенными методами аппроксимации являются метод наименьших квадратов и метод наименьших модулей.
Выбор метода поиска коэффициентов квадратного уравнения зависит от доступных данных и требуемой точности результата. Каждый из перечисленных методов имеет свои преимущества и недостатки, и их выбор обычно основан на конкретной задаче.