Корень числа - это число, возведенное в определенную степень, которая возвращает исходное число. Найти корень числа может быть сложной задачей, особенно если мы не знаем, каким образом это сделать. В данной статье мы рассмотрим несколько методов и подробно объясним, как искать корень числа.
Таблица корней чисел является базовым инструментом для нахождения корня числа. В таблице можно найти числа, их квадраты и кубы, а также корни из этих чисел. Благодаря таблице корней чисел можно легко и быстро найти корни чисел от 1 до 100. Это особенно удобно при решении задач, связанных с геометрией, физикой или математикой.
Как найти корень числа? Существуют различные алгоритмы, позволяющие решить эту задачу. Один из самых простых и распространенных алгоритмов - метод бинарного поиска. Он основывается на принципе деления интервала на две равные части до достижения требуемой точности. Другими словами, алгоритм сначала находит середину интервала, проверяет, является ли значение в данной точке искомым корнем числа, а затем делит интервал на половины до тех пор, пока не будет достигнута необходимая точность.
Зачем нужно находить корень числа

Знание корня числа также полезно при работе с уравнениями и функциями. Например, при решении квадратных уравнений или при аппроксимации функций для получения приближенных значений.
Корень числа также может использоваться для решения задач в финансовой математике, статистике и даже в компьютерной графике и обработке изображений. Например, в статистике он может быть использован для оценки среднеквадратического отклонения или дисперсии данных. В компьютерной графике и обработке изображений корень числа может помочь вычислить интенсивность цвета или яркость пикселя.
Таким образом, нахождение корня числа является важным инструментом для решения различных математических задач и имеет широкое применение в различных областях науки и техники.
Таблица квадратных корней
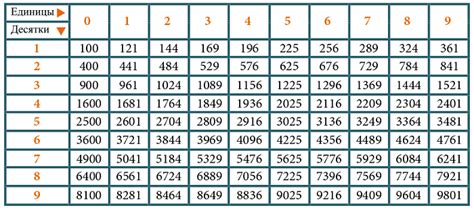
| Исходное число | Квадратный корень |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
С использованием этой таблицы можно легко найти квадратный корень для числа, которое в ней отсутствует. Например, чтобы найти квадратный корень числа 36, мы заметим, что 36 находится между 25 и 49. Тогда можно предположить, что квадратный корень 36 находится между 5 и 7. Путем приближенных вычислений можно найти точное значение 6.
Как найти корень числа вручную

Найти квадратный корень числа можно с помощью нескольких алгоритмов. В этом разделе мы рассмотрим основные методы поиска корня числа без использования калькулятора.
- Метод бинарного поиска:
- Метод Ньютона:
- Метод деления отрезка пополам:
- Метод последовательного приближения:
Для начала определим интервал, в котором находится искомый корень числа. Затем поделим интервал на две половины и выберем ту, в которой находится искомое значение. Затем продолжаем делить интервал на две половины до тех пор, пока не достигнем желаемой точности.
Метод Ньютона является итерационным алгоритмом, который позволяет находить корень функции. Для нахождения корня числа, можно использовать его для функции f(x) = x^2 - n, где n - искомое число. Начинаем с начального приближения x0, затем итерационно находим последовательность x1, x2, ..., xn, пока разница между xn и xn-1 не станет достаточно малой.
Данный метод основан на принципе интервального деления. Начинаем с интервала [a, b], где a и b - начальные значения. Затем находим середину интервала, если середина^2 меньше искомого числа, то заменяем левую границу интервала на середину, иначе заменяем правую границу. Процесс повторяется до тех пор, пока разница между a и b не станет меньше желаемой точности.
Этот метод основан на последовательных приближениях к корню числа. Начинаем с некоторого начального значения, затем вычисляем следующее приближение, используя формулу x(n+1) = (1/2) * (x(n) + (n / x(n))), где n - искомое число. Процесс повторяется до достижения желаемой точности.
Используя эти методы, можно найти корень числа вручную без использования калькулятора. Выбирайте метод, который наиболее удобен и понятен вам.
Метод Ньютона для нахождения корня

Алгоритм метода Ньютона очень прост в использовании:
- Выбрать начальное приближение значения корня.
- Используя выбранное начальное значение, вычислить значение функции и ее производной в этой точке.
- Подставить значение функции и ее производной в формулу:
- Повторять шаги 2 и 3, пока не будет достигнута необходимая точность.
x1 = x0 - (f(x0) / f'(x0))
Метод Ньютона имеет ряд преимуществ в сравнении с другими методами нахождения корня. Он сходится к корню быстрее, чем метод деления пополам, и может быть использован для поиска корней как локальных, так и глобальных функций.
Однако, метод Ньютона требует знания значения производной функции в каждой точке, что может оказаться сложным или невозможным для некоторых функций.
Тем не менее, метод Ньютона остается широко применяемым и эффективным инструментом в численных методах и научных исследованиях.
Примеры вычисления корней чисел

- Корень квадратный из числа 16 равен 4, так как 4 умноженное на 4 равно 16.
- Корень кубический из числа 8 равен 2, так как 2 умноженное на 2 умноженное на 2 равно 8.
- Корень четвертой степени из числа 81 равен 3, так как 3 умноженное на 3 умноженное на 3 умноженное на 3 равно 81.
- Корень пятой степени из числа 32 равен 2, так как 2 умноженное на 2 умноженное на 2 умноженное на 2 умноженное на 2 равно 32.
Для вычисления корней чисел можно использовать различные алгоритмы, такие как метод бисекции, метод Ньютона и метод простых итераций. Каждый из этих методов имеет свои особенности и преимущества в зависимости от вида числа и требуемой точности результата.
Алгоритмы для быстрого вычисления корня числа

Один из самых простых алгоритмов - это метод итераций. Он основан на идее последовательных приближений к искомому корню. Пусть у нас есть число N и мы хотим найти его корень. Сначала выбирается начальное приближение и обозначается как x_0. Затем выполняется итерационный процесс, в ходе которого каждое следующее приближение x_i находится по формуле:
x_i = (x_{i-1} + N/x_{i-1}) / 2
Итерационный процесс продолжается до тех пор, пока разница между двумя соседними приближениями x_i и x_{i-1} не становится меньше заданной точности.
Еще одним алгоритмом, используемым для быстрого вычисления корня числа, является метод Ньютона. Он также основан на итерациях, но использует более сложные вычисления. Идея состоит в том, чтобы найти корень уравнения f(x) = 0, где f(x) - функция, заданная формулой f(x) = x^2 - N. Алгоритм состоит из следующих шагов:
Шаг 1: Выбрать начальное приближение x_0.
Шаг 2: Вычислить значение функции f(x) для текущего приближения x_i.
Шаг 3: Вычислить производную функции f(x) по переменной x и обозначить ее как f'(x).
Шаг 4: Вычислить следующее приближение x_{i+1} по формуле:
x_{i+1} = x_i - f(x_i) / f'(x_i)
Шаг 5: Повторять шаги 2-4, пока разница между двумя соседними приближениями x_i и x_{i+1} не станет меньше заданной точности.
Эти алгоритмы позволяют эффективно вычислить корень числа и достичь желаемой точности. Они широко используются в программировании, например, для решения уравнений или оптимизации функций.