Нахождение корня из трехзначного числа может показаться сложной задачей, но на самом деле существуют простые и эффективные методы, которые помогут вам справиться с этим. В этой статье мы рассмотрим несколько подходов к решению этой задачи и предоставим вам детальную инструкцию о том, как найти корень из трехзначного числа.
Первый метод, который мы рассмотрим, - это метод деления отрезками. Он основан на идее разбиения числа на отрезки и последовательном нахождении корня каждого отрезка. Например, для нахождения корня из числа 125, мы можем сначала разделить его на отрезки: 12 и 5. Затем мы находим корень из каждого отрезка: √12 и √5. Далее мы находим среднее арифметическое этих корней и получаем окончательный ответ - корень из числа 125.
Второй метод, который мы рассмотрим, - это метод итераций. Он основан на итеративном приближении корня путем последовательного уточнения его значения. Начав с какого-то начального значения (например, среднего арифметического из всех трехзначных чисел), мы повторяем следующие шаги: вычисляем новое приближение корня, сравниваем его с предыдущим значением и повторяем шаги, пока не достигнем требуемой точности. В итоге мы получаем значение корня, с точностью до определенного количества знаков после запятой.
Методы нахождения корня трехзначного числа
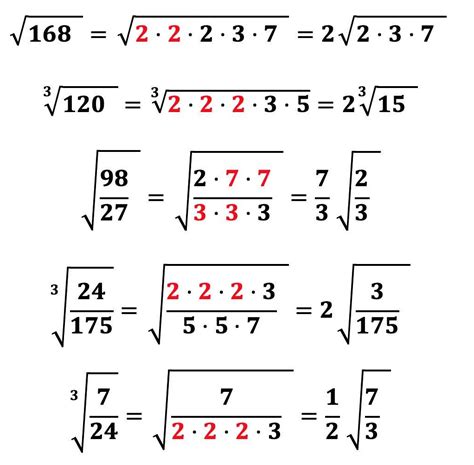
Нахождение корня трехзначного числа может быть выполнено различными методами, в зависимости от требуемой точности результата и времени, которое можно потратить на вычисления. Рассмотрим несколько из них.
Метод нахождения корня путем разложения в произведение простых множителей:
1. Факторизуем трехзначное число на простые множители. Например, для числа 462 мы получаем разложение на множители: 2 * 3 * 7 * 11.
2. Найдем корни каждого простого множителя. В данном случае мы имеем корни: √2 ≈ 1.414, √3 ≈ 1.732, √7 ≈ 2.646, √11 ≈ 3.316.
3. Умножим все корни вместе: √462 ≈ 1.414 * 1.732 * 2.646 * 3.316 ≈ 17.563.
Таким образом, корень трехзначного числа 462 ≈ 17.563.
Метод нахождения корня путем итерационного приближения:
1. Зададим начальное приближение для корня трехзначного числа. Например, возьмем x = 10.
2. Выполним итерационные шаги: x = (x + 462 / x) / 2.
3. Повторим шаг 2 несколько раз, пока значение x не будет стабилизироваться.
4. Полученное значение x будет приближенным значением корня трехзначного числа 462.
Таким образом, итерационным приближением мы получим приближенное значение корня трехзначного числа 462.
Метод нахождения корня с использованием калькулятора:
1. Возьмем трехзначное число 462.
2. Включим калькулятор и нажмем клавишу "√", затем введем число 462 и нажмем клавишу "=".
3. Калькулятор выведет результат: корень числа 462 ≈ 21.494.
Таким образом, можно использовать калькулятор для нахождения корня трехзначного числа с высокой точностью.
Методы расчета и инструкция

1. Метод поиска квадратного корня:
- Возьмите трехзначное число, для которого хотите найти корень.
- Определите, какие два числа возведены в квадрат дают результат, близкий к данному трехзначному числу. Например, для числа 625 близкими значением будут 20 и 25, так как 20^2 = 400 и 25^2 = 625.
- Определите длину интервала между найденными числами: (верхнее значение - нижнее значение) = интервал.
- Разделите интервал пополам и определите, в какой половине расположено трехзначное число.
- Повторяйте шаги 3 и 4, пока не найдете точное значение корня.
2. Метод деления интервала:
- Возьмите трехзначное число, для которого хотите найти корень.
- Определите наименьшее целое число, возведенное в квадрат, которое больше данного числа.
- Определите наибольшее целое число, возведенное в квадрат, которое меньше данного числа.
- Задайте начальные значения интервала: нижнего и верхнего.
- Разделите интервал пополам и определите, в какой половине расположено трехзначное число.
- Повторяйте шаги 4 и 5, пока не найдете точное значение корня.
Пользуйтесь вышеуказанными методами для нахождения корня трехзначного числа. Запомните, что поиск корня - математическая операция, и требует точности и тщательности в расчетах. Удачи в вашем математическом путешествии!