Решение уравнений – одно из базовых умений в математике, на котором строятся дальнейшие знания и навыки. Особую роль играют уравнения восьмого класса, которые требуют более сложных методов решения и понимания. В данной статье мы подробно рассмотрим, как найти корень уравнения восьмого класса через дискриминант.
Дискриминант – это показатель, который определяет количество и характер корней уравнения. В случае, когда дискриминант равен нулю, у уравнения есть один корень. Если дискриминант положителен, то имеются два различных корня. В случае, когда дискриминант отрицателен, корней нет.
Для нахождения корней уравнения посредством дискриминанта, необходимо выполнить несколько шагов. Сначала нужно выписать коэффициенты уравнения (a, b и c), затем рассчитать дискриминант по формуле D = b^2 - 4ac. Далее, используя найденное значение дискриминанта, мы можем определить количество и характер корней, а затем найти сами корни по формулам x1 = (-b + √D) / 2a и x2 = (-b - √D) / 2a.
Как найти корень уравнения в 8 классе

Для начала, вспомним, что квадратное уравнение имеет следующий вид: ax^2 + bx + c = 0, где a, b и c - это коэффициенты, которые могут быть любыми числами. Наша задача - найти значения x, при которых уравнение будет верно.
Если дискриминант D равен нулю, то уравнение имеет один корень: x = -b/2a. Если D больше нуля, то уравнение имеет два различных корня: x1 = (-b + √D) / 2a и x2 = (-b - √D) / 2a. Если D меньше нуля, то уравнение не имеет действительных корней.
Важно отметить, что при решении уравнения необходимо учитывать знаки коэффициентов a, b и c. Также важно следить за правильным использованием математических операций и порядка действий.
Приведем пример для наглядности. Рассмотрим уравнение x^2 - 4x + 3 = 0. В данном случае a = 1, b = -4 и c = 3. Вычислим дискриминант: D = (-4)^2 - 4 * 1 * 3 = 16 - 12 = 4. Поскольку D больше нуля, уравнение имеет два корня: x1 = (4 + √4) / 2 * 1 = (4 + 2) / 2 = 6 / 2 = 3 и x2 = (4 - √4) / 2 * 1 = (4 - 2) / 2 = 2 / 2 = 1.
Таким образом, корни данного уравнения равны x1 = 3 и x2 = 1.
Простое объяснение и шаги решения через дискриминант
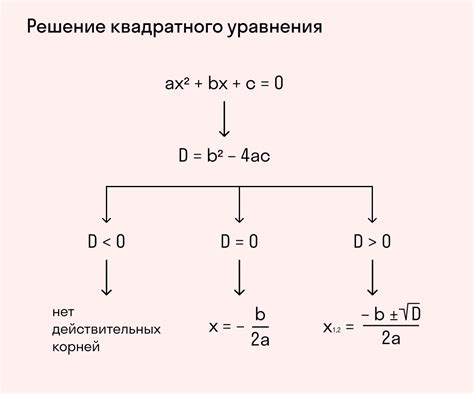
Для нахождения корня уравнения восьмого класса через дискриминант необходимо следовать нескольким простым шагам. Рассмотрим подробнее, что такое дискриминант и как его использовать.
Дискриминант - это число, которое определяется по формуле Δ = b^2 - 4ac, где a, b и c - коэффициенты уравнения вида ax^2 + bx + c = 0. Значение дискриминанта позволяет определить количество и тип корней уравнения.
Шаги решения уравнения через дискриминант:
| Значение дискриминанта (Δ) | Количество и тип корней |
|---|---|
| Δ > 0 | Уравнение имеет два различных вещественных корня. |
| Δ = 0 | Уравнение имеет один вещественный корень (корень кратности 2). |
| Δ < 0 | Уравнение не имеет вещественных корней, только комплексные. |
1. Подставьте значения коэффициентов a, b и c в формулу дискриминанта: Δ = b^2 - 4ac.
2. Вычислите значение дискриминанта.
3. Определите количество и тип корней уравнения, используя таблицу выше.
4. В случае наличия вещественных корней, для их нахождения используйте формулу: x = (-b ± √Δ) / (2a).
Теперь вы знаете, как найти корень уравнения восьмого класса через дискриминант. Следуйте этим простым шагам и вы сможете успешно решать такие задачи.
Что такое уравнение в 8 классе?
Решение уравнений является одной из основных задач алгебры, и восьмиклассники изучают различные методы решения уравнений, в том числе и с использованием дискриминанта.
Для решения уравнения восьмиклассникам необходимо выполнить следующие шаги:
- Привести уравнение к виду, в котором все члены с переменной находятся в левой части, а все числа - в правой.
- Использовать разные методы решения уравнений, например, метод подстановки, метод равенства нулю или метод приведения подобных членов.
- Если в уравнение присутствует квадрат и неизвестная величина возведена в степень 2, можно применить формулу дискриминанта для нахождения корней.
- Проверить полученные корни, подставив их в исходное уравнение, чтобы убедиться, что они удовлетворяют его условиям.
Математика восьмого класса дает базовые знания и навыки для решения простых уравнений, а в дальнейшем, в старших классах, эти навыки будут развиваться и расширяться для решения более сложных математических проблем.
Определение и примеры

Рассмотрим пример простого уравнения: x + 2 = 5. Чтобы найти корень, нужно найти значение переменной x, при котором это уравнение будет верным. В данном случае, если мы вычтем 2 с обеих сторон уравнения, получим x = 3. Таким образом, корнем этого уравнения является число 3.
Корень уравнения может быть один, несколько или не существовать вовсе. Например, уравнение x^2 - 5x + 6 = 0 имеет два корня: x=2 и x=3. Эти значения переменной делают уравнение верным. С другой стороны, уравнение x^2 + 1 = 0 не имеет решений, так как не существует такого значения переменной, которое сделало бы его верным.
Важно отметить, что для решения уравнений более высокого порядка существует специальные методы, такие как методы факторизации и методы выделения полного квадрата. Однако для простых уравнений первой степени, решение может быть найдено путем простых арифметических операций.
Как найти корень уравнения в 8 классе?

На уроках алгебры в 8 классе изучается метод решения квадратных уравнений. Для того чтобы найти корни уравнения, нужно выполнить несколько шагов:
- Запишите уравнение вида ax^2 + bx + c = 0, где a, b и c - коэффициенты уравнения.
- Вычислите дискриминант уравнения по формуле D = b^2 - 4ac.
- Если дискриминант D больше нуля, то уравнение имеет два действительных корня. Вычислите эти корни по формуле x1 = (-b + √D) / 2a и x2 = (-b - √D) / 2a.
- Если дискриминант D равен нулю, то уравнение имеет один действительный корень. Вычислите этот корень по формуле x = -b / 2a.
- Если дискриминант D меньше нуля, то уравнение не имеет действительных корней.
Итак, при решении квадратного уравнения в 8 классе необходимо знать коэффициенты уравнения, вычислить дискриминант и применить соответствующую формулу для нахождения корней.
Ниже приведена таблица, демонстрирующая различные значения дискриминанта и количество корней уравнения:
| Значение дискриминанта D | Количество корней |
|---|---|
| D > 0 | 2 |
| D = 0 | 1 |
| D | 0 |
Используя эти шаги и таблицу, вы сможете легко найти корни квадратного уравнения в 8 классе. Помните, что практика и тренировка помогут вам совершенствовать свои навыки в решении уравнений.
Общий подход и шаги плана решения
Для нахождения корня уравнения восьмого класса следуйте следующим шагам:
| Шаг 1: | Запишите уравнение вида ax^2 + bx + c = 0, где a, b и c - коэффициенты. |
| Шаг 2: | Вычислите дискриминант по формуле D = b^2 - 4ac. |
| Шаг 3: | Определите тип корней, исходя из значения дискриминанта:
|
| Шаг 4: | Используя формулу x = (-b ± √D) / 2a, вычислите значения корней. |
| Шаг 5: | Проверьте полученные значения, подставив их обратно в уравнение. Решение должно удовлетворять исходному уравнению. |
Следуя этим шагам, вы сможете решить уравнение восьмого класса и найти его корень.
Что такое дискриминант уравнения?
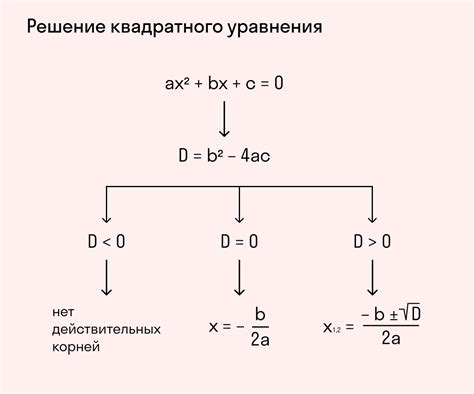
Д = b² - 4ac
где а, b и с - это коэффициенты квадратного уравнения типа:
ax² + bx + c = 0
Дискриминант может принимать три значения:
- Если дискриминант больше нуля (Д > 0), то у уравнения два различных вещественных корня;
- Если дискриминант равен нулю (Д = 0), то у уравнения есть один вещественный корень;
- Если дискриминант меньше нуля (Д
Дискриминант позволяет определить, какие типы решений может иметь квадратное уравнение и помогает в нахождении корней. Также он используется для выяснения свойств и формы графика квадратного уравнения.
Определение и значение

Нахождение корня уравнения является фундаментальным понятием в алгебре и математике. Это позволяет решать различные задачи, связанные с нахождением неизвестного значения или точки пересечения графика с осью абсцисс.
Оценка корня уравнения важна в многих областях науки, техники и экономики. Например, она может использоваться для нахождения решений уравнений движения, вычисления вероятностей или определения оптимальных значений в задачах оптимизации.
Нахождение корня уравнения может быть выполнено с использованием различных методов, включая метод подстановки, метод итераций или метод Ньютона. Один из наиболее известных способов нахождения корней уравнений - использование дискриминанта.
Как определить существование корней через дискриминант?

Дискриминант вычисляется по формуле D = b^2 - 4ac, где b - коэффициент при x, a - коэффициент при x^2 и c - свободный член.
Если дискриминант больше нуля, то уравнение имеет два различных корня: x1 = (-b + √D) / (2a) и x2 = (-b - √D) / (2a).
Если дискриминант равен нулю, то уравнение имеет один корень: x = -b / (2a).
Если дискриминант меньше нуля, то уравнение не имеет решений.
Таким образом, использование понятия дискриминанта позволяет определить тип решений уравнения и найти значения корней, если они существуют.
Алгоритм и примеры
Для нахождения корня уравнения восьмого класса с помощью дискриминанта следуйте следующим алгоритмом:
- Запишите уравнение в виде ax^2 + bx + c = 0, где a, b и c - это коэффициенты уравнения.
- Вычислите дискриминант по формуле D = b^2 - 4ac.
- Если D > 0, то уравнение имеет два различных корня.
- Если D = 0, то уравнение имеет один корень.
- Если D
- Вычислите корни уравнения по формулам x1 = (-b + sqrt(D)) / (2a) и x2 = (-b - sqrt(D)) / (2a).
Примеры:
- Пример 1: Решим уравнение 2x^2 - 5x - 3 = 0.
- Пример 2: Решим уравнение x^2 + 8x + 16 = 0.
Здесь a = 2, b = -5 и c = -3.
Вычисляем дискриминант: D = (-5)^2 - 4 * 2 * (-3) = 25 + 24 = 49.
Так как D > 0, уравнение имеет два различных корня.
Вычисляем корни: x1 = (-(-5) + sqrt(49)) / (2 * 2) = (5 + 7) / 4 = 3.
x2 = (-(-5) - sqrt(49)) / (2 * 2) = (5 - 7) / 4 = -1/2.
Корни уравнения: x1 = 3 и x2 = -1/2.
Здесь a = 1, b = 8 и c = 16.
Вычисляем дискриминант: D = 8^2 - 4 * 1 * 16 = 64 - 64 = 0.
Так как D = 0, уравнение имеет один корень.
Вычисляем корень: x = (-8 + sqrt(0)) / (2 * 1) = (-8 + 0) / 2 = -4.
Корень уравнения: x = -4.
Как найти значения корней через дискриминант?

Для нахождения корней уравнения через дискриминант необходимо следовать нескольким шагам:
- Записать уравнение в виде ax^2 + bx + c = 0, где a, b и c - коэффициенты уравнения.
- Вычислить дискриминант по формуле D = b^2 - 4ac, где D - дискриминант.
- Если дискриминант больше нуля (D > 0), то уравнение имеет два различных корня.
- Если дискриминант равен нулю (D = 0), то уравнение имеет один корень.
- Если дискриминант меньше нуля (D
- Если уравнение имеет корни, то значения корней можно найти с помощью формулы:
x1 = (-b + √D) / (2a)
x2 = (-b - √D) / (2a)
Где x1 и x2 - значения корней уравнения, √D - корень из дискриминанта.
Таким образом, решение уравнения через дискриминант позволяет найти значения корней и определить их количество.
Формулы и вычисления
Когда дискриминант положительный (D > 0), уравнение имеет два действительных корня, которые можно найти с помощью формулы:
x1 = (-b + √D) / 2a
x2 = (-b - √D) / 2a
Когда дискриминант равен нулю (D = 0), уравнение имеет один действительный корень, который можно найти с помощью формулы:
x = -b / 2a
Когда дискриминант отрицательный (D
Чтобы найти корни уравнения, следует выполнить следующие шаги:
- Вычислить значение дискриминанта D = b^2 - 4ac.
- Проверить значение дискриминанта:
- Если D > 0, рассчитать x1 и x2 по формулам выше.
- Если D = 0, рассчитать x по формуле выше.
- Если D
Эти шаги помогут вам найти корни уравнения и проверить правильность решения.