Методы поиска корреляции в Python

Корреляция – это понятие из области статистики, которое позволяет определить степень зависимости между двумя или более переменными. В Python существует несколько методов, которые позволяют вычислить корреляцию для набора данных.

Один из самых распространенных методов для поиска корреляции в Python – это коэффициент корреляции Пирсона. Этот метод позволяет определить линейную взаимосвязь между двумя переменными. Коэффициент корреляции Пирсона может принимать значения от -1 до 1, где значение 1 означает положительную линейную корреляцию, значение -1 – отрицательную, а значение 0 – отсутствие корреляции.

Еще один метод, который позволяет определить связь между переменными, – это коэффициент корреляции Спирмена. Этот метод не зависит от закона распределения переменных и позволяет выявить не только линейную, но и монотонную взаимосвязь. Коэффициент корреляции Спирмена также может принимать значения от -1 до 1.

Кроме того, в Python существуют другие методы для поиска корреляции, такие как коэффициент корреляции Кендалла, который определяет зависимость между рангами переменных, и коэффициент детерминации, который показывает, насколько хорошо линейная модель подходит для предсказания зависимой переменной.

Что такое корреляция?

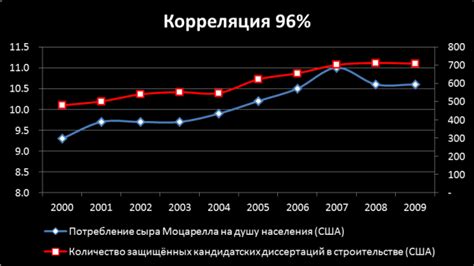
Корреляция применяется для изучения и сравнения данных и может быть положительной или отрицательной. Положительная корреляция указывает на то, что при увеличении значений одной переменной также увеличиваются значения другой переменной. Напротив, отрицательная корреляция показывает, что при увеличении значений одной переменной значения другой переменной уменьшаются.

Коэффициент корреляции - это числовая мера, которая показывает силу и направление корреляции между переменными. Он может принимать значения от -1 до 1. Если коэффициент корреляции равен 1, значит, есть положительная линейная связь между переменными. Если он равен -1, то есть отрицательная линейная связь. Коэффициент корреляции, равный 0, означает отсутствие связи между переменными.

Корреляционный анализ помогает нам понять, какие переменные влияют друг на друга и насколько сильно. Он используется в различных областях, таких как экономика, социология, медицина, психология и многих других.

Математическое определение корреляции и ее роль в статистике

Математически корреляция определяется с помощью коэффициента корреляции, который может принимать значения от -1 до 1. Значение -1 означает полную обратную зависимость, 0 - отсутствие взаимосвязи, а 1 - полную прямую зависимость.

Коэффициент корреляции можно вычислить для различных типов данных, например, для числовых переменных или бинарных переменных. Он может быть вычислен с использованием различных методов, таких как Пирсона, Спирмена или Кендалла.

Роль корреляции в статистике заключается в том, что она позволяет нам понять, насколько сильна связь между переменными и как она может быть использована для предсказания или анализа данных. Корреляция также может помочь нам выявить скрытые зависимости между переменными и определить влияние факторов на исследуемый процесс или явление.

Использование методов поиска корреляции в Python позволяет нам эффективно анализировать большие объемы данных и находить в них скрытые закономерности и зависимости. Это полезный инструмент для исследователей, аналитиков данных и специалистов в области статистики.

Каким образом можно найти корреляцию в Python?

Python предоставляет множество инструментов для анализа данных, включая возможность расчета и визуализации корреляции.

Для начала, можно использовать библиотеку pandas для импорта и обработки данных. После того, как данные загружены и представлены в виде таблицы, можно использовать метод .corr() для расчета корреляции между различными переменными.

Например:

import pandas as pd
# Загрузка данных из файла
data = pd.read_csv("data.csv")
# Расчет корреляции между двумя переменными
correlation = data["variable1"].corr(data["variable2"])
print("Коэффициент корреляции:", correlation)

Кроме того, можно использовать метод .corr() для расчета матрицы корреляции между несколькими переменными:

# Расчет матрицы корреляции между несколькими переменными
correlation_matrix = data.corr()
print(correlation_matrix)

Полученная матрица корреляции можно визуализировать с помощью библиотеки seaborn:

import seaborn as sns
# Визуализация матрицы корреляции
sns.heatmap(correlation_matrix, annot=True)
plt.show()

Этот график позволяет исследовать взаимосвязи между различными переменными и определить силу и направление их корреляционной связи.

Кроме того, можно использовать библиотеку scipy для расчета различных статистических показателей, включая корреляцию. Например, функция pearsonr() из модуля scipy.stats может быть использована для расчета коэффициента корреляции Пирсона и его значимости:

from scipy.stats import pearsonr
# Расчет коэффициента корреляции Пирсона и его значимости
correlation, p_value = pearsonr(data["variable1"], data["variable2"])
print("Коэффициент корреляции:", correlation)
print("Значимость:", p_value)

Таким образом, Python предоставляет разнообразные инструменты для расчета и визуализации корреляции. Они позволяют анализировать связи между переменными и выявлять важные зависимости в данных.

Метод корреляционного анализа в Pandas

Метод corr() может быть применен к объектам Series или DataFrame и возвращает таблицу корреляции. Значения коэффициентов корреляции находятся в диапазоне от -1 до 1, где -1 указывает на полное отрицательное влияние, 0 - на отсутствие корреляции, а 1 - на положительное влияние.

Пример использования метода corr():

import pandas as pd
# создаем DataFrame с данными
data = {'Первая переменная': [1, 2, 3, 4, 5],
'Вторая переменная': [2, 4, 6, 8, 10],
'Третья переменная': [3, 6, 9, 12, 15]}
df = pd.DataFrame(data)
# рассчитываем корреляцию между столбцами
corr_matrix = df.corr()
print(corr_matrix)

Результатом будет таблица корреляции:

                    Первая переменная  Вторая переменная  Третья переменная
Первая переменная            1.000000          1.000000           1.000000
Вторая переменная            1.000000          1.000000           1.000000
Третья переменная            1.000000          1.000000           1.000000

В данном примере все значения коэффициентов корреляции равны 1, что означает идеальную положительную корреляцию между всеми переменными.

Метод корреляционного анализа в Pandas позволяет быстро и удобно определить степень связи между двумя или более переменными в наборе данных. Это может быть полезным в задачах анализа, прогнозирования или машинного обучения.

Использование библиотеки Pandas для вычисления корреляции

Библиотека Pandas предоставляет мощные инструменты для работы с данными, включая возможность вычисления корреляции между различными переменными. Это важный инструмент для анализа данных, который позволяет найти связи и зависимости между различными переменными.

Для вычисления корреляции с помощью Pandas необходимо импортировать эту библиотеку:

import pandas as pd

Затем можно создать DataFrame - структуру данных, предоставляемую Pandas, для хранения и обработки данных. DataFrame может быть создан из различных источников данных, таких как CSV-файлы, Excel-файлы или SQL-запросы. В данном случае, предположим, что у нас уже есть DataFrame с именем "data" и двумя столбцами "x" и "y", которые содержат числовые значения:

data = pd.DataFrame({
'x': [1, 2, 3, 4, 5],
'y': [2, 4, 6, 8, 10]
})

Чтобы вычислить корреляцию между столбцами "x" и "y", мы можем использовать функцию corr() из библиотеки Pandas:

correlation = data['x'].corr(data['y'])

Эта функция возвращает коэффициент корреляции Пирсона, который является мерой линейной зависимости между двумя переменными. Коэффициент корреляции может принимать значения от -1 до 1. Значение 1 означает положительную линейную зависимость, значение -1 означает отрицательную линейную зависимость, а значение 0 означает отсутствие линейной зависимости.

Кроме того, библиотека Pandas предоставляет функцию corr() для вычисления матрицы корреляции. Матрица корреляции показывает зависимость каждой пары переменных в DataFrame. Например, чтобы вычислить матрицу корреляции для всех столбцов DataFrame "data", мы можем использовать следующий код:

correlation_matrix = data.corr()

Результатом будет DataFrame, где строки и столбцы представляют собой имена переменных, а значения - коэффициенты корреляции.

Использование библиотеки Pandas для вычисления корреляции позволяет провести анализ взаимосвязей между переменными на основе имеющихся данных. Это полезный инструмент для исследования данных и принятия информированных решений.

Метод коэффициента корреляции Пирсона

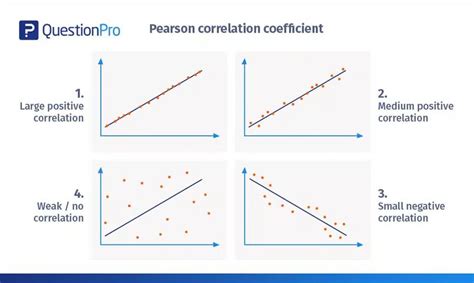
Коэффициент корреляции Пирсона может принимать значения от -1 до 1. Знак коэффициента указывает на направление связи: положительный коэффициент указывает на положительную связь (чем больше значение одной переменной, тем больше значение другой переменной), отрицательный коэффициент указывает на отрицательную связь (чем больше значение одной переменной, тем меньше значение другой переменной), и нулевой коэффициент указывает на отсутствие связи.

Для расчета коэффициента корреляции Пирсона в Python можно воспользоваться функцией corrcoef из библиотеки NumPy. Эта функция принимает два массива числовых значений и возвращает ковариационную матрицу, из которой можно извлечь коэффициент корреляции Пирсона.

Пример кода для расчета коэффициента корреляции Пирсона:

import numpy as np
# Создание массивов с числовыми значениями
x = np.array([1, 2, 3, 4, 5])
y = np.array([6, 7, 8, 9, 10])
# Расчет коэффициента корреляции Пирсона
corr_matrix = np.corrcoef(x, y)
corr_coefficient = corr_matrix[0, 1]
print("Коэффициент корреляции Пирсона:", corr_coefficient)

Коэффициент корреляции Пирсона является мощным инструментом для измерения связи между двумя переменными и широко используется в статистическом анализе данных. Его применение позволяет выявить и оценить силу и направление связи между переменными, что может быть полезно для прогнозирования и принятия решений.

Преимущества	Недостатки
Простота расчета и интерпретации	Не учитывает нелинейные связи
Широкое применение	Чувствителен к выбросам
Позволяет оценивать силу связи	Не учитывает взаимосвязь с другими переменными

Описание коэффициента корреляции Пирсона и его применение

Коэффициент корреляции Пирсона вычисляется по формуле:

r = (Σ((x - x̄)(y - ȳ))) / (√(Σ(x - x̄)²) * √(Σ(y - ȳ)²))

где:

r - коэффициент корреляции Пирсона
x, y - значения переменных
x̄, ȳ - средние значения переменных
Σ - сумма значений

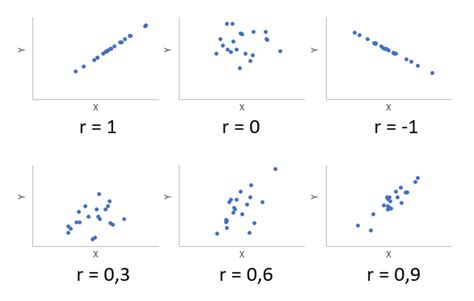
Значение коэффициента корреляции Пирсона может находиться в диапазоне от -1 до 1. Чем ближе значение к 1 или -1, тем сильнее линейная связь. Значение 1 означает положительную линейную связь, значение -1 - отрицательную, а значение 0 - отсутствие связи.

Коэффициент корреляции Пирсона часто используется для исследования зависимости между датасетами. Он может помочь в понимании, насколько сильно две переменные взаимосвязаны и может использоваться для прогнозирования значений одной переменной на основании другой.

Также коэффициент корреляции Пирсона позволяет определить направление и силу связи между переменными. Если значение положительно, это означает, что значения переменных растут вместе. Если значение отрицательно, это означает, что значения переменных меняются в противоположных направлениях.

Как найти корреляцию между данными с помощью Python-методов