Косинус между прямой и плоскостью является важной характеристикой их взаимного положения в трехмерном пространстве. Такое положение может быть полностью определено с помощью геометрических методов и специальных формул.
Прямая и плоскость - это два основных объекта геометрии, которые часто встречаются в математическом анализе и физике. Знание угла между ними может помочь решить различные задачи, связанные с определением взаимного положения объектов в пространстве.
Один из способов вычисления косинуса между прямой и плоскостью состоит в использовании скалярного произведения векторов. Сначала необходимо задать прямую и плоскость в виде уравнений или их параметрических представлений. Затем необходимо векторно умножить вектор-нормаль плоскости на направляющий вектор прямой. После этого рассчитывается длина этих векторов и производится деление на произведение их длин, что позволяет получить косинус угла между ними.
Что такое косинус и зачем он нужен?
Зачем нам нужно знать косинус? Косинус позволяет нам вычислять углы, расстояния и отклонения в различных задачах и моделях. Например, в геометрии он используется для измерения углов между прямыми и плоскостями. Кроме того, косинус может быть полезен при решении задач в физике, инженерии, графике, компьютерной графике и других областях.
Вычисление косинуса может быть осуществлено при помощи тригонометрической таблицы или калькулятора. Однако, существуют специальные формулы и методы для вычисления косинуса через другие тригонометрические функции, что может быть удобно при решении сложных задач.
| Угол | Косинус |
|---|---|
| 0° | 1 |
| 30° | √3/2 |
| 45° | √2/2 |
| 60° | 1/2 |
| 90° | 0 |
Таким образом, знание косинуса и его свойств может значительно упростить вычисления и решение задач, связанных с геометрией и тригонометрией, а также использоваться в различных областях науки и техники.
Как найти косинус между прямой и плоскостью?
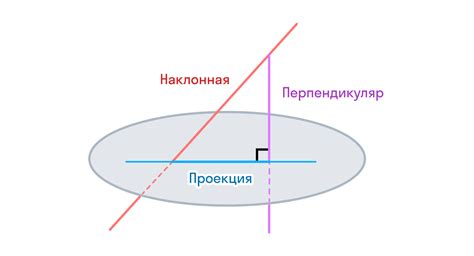
Когда мы работаем с пространственной геометрией, нам может потребоваться вычислить косинус угла между прямой и плоскостью. Это может быть полезно, например, при решении задач нахождения угловых отношений в трехмерном пространстве.
Существуют несколько подходов и формул для решения этой задачи. Один из таких подходов - использование векторов.
Представим прямую в параметрической форме:
- x = x0 + a*t
- y = y0 + b*t
- z = z0 + c*t
Здесь (x0, y0, z0) - точка, через которую проходит прямая, (a, b, c) - направляющий вектор прямой, t - параметр, изменяющийся в интервале (-∞, +∞).
Плоскость можно представить уравнением:
A*x + B*y + C*z + D = 0
Чтобы найти косинус между прямой и плоскостью, можно воспользоваться следующей формулой:
cos(θ) = |(a*A + b*B + c*C)/(sqrt(a^2 + b^2 + c^2) * sqrt(A^2 + B^2 + C^2))|
Здесь θ - угол между прямой и плоскостью, (a, b, c) - координаты направляющего вектора прямой, (A, B, C) - коэффициенты уравнения плоскости.
Вычисление косинуса между прямой и плоскостью позволяет определить, насколько эти геометрические объекты близки друг к другу или насколько они сонаправлены. Это может быть полезным для решения различных математических и физических задач, связанных с трехмерной геометрией.
Метод нахождения косинуса через проекции

Для начала необходимо определить вектор направления прямой и вектор нормали плоскости. Затем найдем проекцию вектора направления прямой на вектор нормали плоскости. Далее выразим модуль проекции вектора через модули векторов направления прямой и нормали плоскости. Косинус угла между прямой и плоскостью будет равен отношению модуля проекции к произведению модулей векторов направления и нормали.
Формула для нахождения косинуса через проекции:
cos(угол) = проекция / (|вектор_направления| * |вектор_нормали|)
Где:
- cos(угол) - косинус угла между прямой и плоскостью;
- проекция - проекция вектора направления прямой на вектор нормали плоскости;
- |вектор_направления| - модуль вектора направления прямой;
- |вектор_нормали| - модуль вектора нормали плоскости.
Используя данный метод, можно вычислить косинус угла между прямой и плоскостью и использовать полученный результат в различных задачах геометрии и физики.
Метод нахождения косинуса через уравнение плоскости
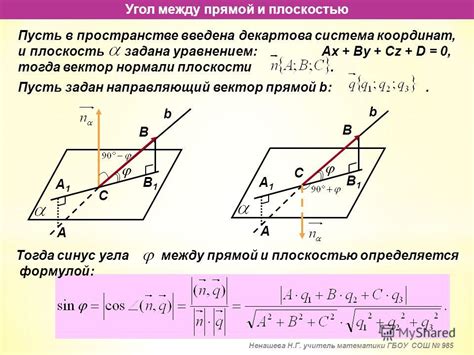
Для нахождения косинуса между прямой и плоскостью можно использовать метод, основанный на уравнении плоскости. Уравнение плоскости задается в виде:
| Ax + By + Cz + D = 0 |
где A, B и C - коэффициенты, определяющие нормальный вектор плоскости, а D - свободный член.
Нормальный вектор плоскости можно найти как вектор, состоящий из коэффициентов A, B и C. Для этого нормируем вектор, поделив его на его длину:
| n = (A, B, C) / sqrt(A^2 + B^2 + C^2) |
Прямая, заданная параметрическим уравнением:
| x = x0 + at |
| y = y0 + bt |
| z = z0 + ct |
где x0, y0 и z0 - координаты начальной точки прямой, a, b и c - направляющие коэффициенты прямой, а t - параметр.
Подставим координаты прямой в уравнение плоскости и получим:
| A(x0 + at) + B(y0 + bt) + C(z0 + ct) + D = 0 |
Раскроем скобки и приведем подобные слагаемые:
| (Ax0 + By0 + Cz0 + D) + (Aa + Bb + Cc)t = 0 |
Находим значение переменной t:
| t = - (Ax0 + By0 + Cz0 + D) / (Aa + Bb + Cc) |
Теперь можно найти направляющий вектор прямой:
| v = (a, b, c) |
Нормируем этот вектор:
| v = v / sqrt(a^2 + b^2 + c^2) |
Косинус угла между векторами можно найти как скалярное произведение нормализованного направляющего вектора прямой и нормального вектора плоскости:
| cosine = v * n = a*A + b*B + c*C / sqrt(a^2 + b^2 + c^2) * sqrt(A^2 + B^2 + C^2) |
Таким образом, метод нахождения косинуса между прямой и плоскостью через уравнение плоскости заключается в нахождении коэффициентов уравнения плоскости, нахождении значения параметра t, нахождении направляющего вектора прямой и последующем нахождении косинуса угла между векторами.
Формулы для вычисления косинуса

1. Формула косинуса через скалярное произведение
Одним из способов расчета косинуса между прямой и плоскостью является использование формулы косинуса через скалярное произведение векторов. Данная формула имеет вид:
cos(θ) = (A·B) / (|A|·|B|)
где A и B - векторы, а |A| и |B| - их длины. Скалярное произведение векторов равно сумме произведений соответствующих координат векторов.
2. Формула косинуса через координаты
Другой способ расчета косинуса между прямой и плоскостью основан на использовании координат точек, через которые проходят прямая и плоскость. Формула имеет вид:
cos(θ) = (Ax·Bx + Ay·By + Az·Bz) / (|A|·|B|)
где Ax, Ay, Az - координаты точки на прямой, Bx, By, Bz - координаты точки на плоскости, а |A| и |B| - длины соответствующих векторов.
Эти формулы позволяют точно вычислить косинус между прямой и плоскостью, что может быть полезным при решении геометрических задач или в применении в научных и технических расчетах.
Формула косинуса через скалярное произведение векторов

Косинус между прямой и плоскостью можно найти с помощью формулы, основанной на скалярном произведении векторов.
Пусть у нас есть прямая, заданная двумя точками A и B, и плоскость, заданная общим уравнением Ax + By + Cz + D = 0. Чтобы найти косинус между прямой и плоскостью, нужно сначала найти вектор, параллельный прямой, и вектор, нормальный плоскости.
Вектор, параллельный прямой, можно найти вычислив разность координат векторов AB = (xB - xA, yB - yA, zB - zA).
Вектор, нормальный плоскости, можно найти, зная коэффициенты общего уравнения плоскости: n = (A, B, C).
Затем вычисляем скалярное произведение векторов AB и n: AB * n = (xB - xA) * A + (yB - yA) * B + (zB - zA) * C.
Косинус между прямой и плоскостью можно найти, разделив полученное скалярное произведение на произведение длин векторов AB и n: cos(θ) = (AB * n) / (|AB| * |n|).
Таким образом, формула косинуса для нахождения угла между прямой и плоскостью через скалярное произведение векторов имеет вид: cos(θ) = (AB * n) / (|AB| * |n|).