Котангенс является одним из основных тригонометрических понятий, которое широко используется в математике, физике и инженерных науках. Он представляет собой отношение сторон прямоугольного треугольника и вычисляется как обратное тангенсу угла в этом треугольнике.
Но как найти котангенс, если у нас есть только единичная окружность? Геометрическое определение котангенса основывается на свойствах единичной окружности и знании угла, который нужно вычислить.
Чтобы найти котангенс, необходимо провести радиус окружности до точки касания с осью OX и построить прямую линию, соединяющую начало координат (центр окружности) с точкой касания. Затем измеряем длины линий на графике и используем их для вычисления котангенса с помощью формулы.
Таким образом, геометрическое определение котангенса на единичной окружности позволяет нам получить точные значения этой тригонометрической функции и использовать их для решения различных геометрических и математических задач.
Что такое котангенс?

Для любого угла α, где 0 < α < 90 градусов, котангенс вычисляется как:
cot(α) = 1/tan(α)
Значения котангенса находятся в интервале от -∞ до +∞.
Как и другие тригонометрические функции, котангенс широко применяется в математике, физике, инженерии и других науках для решения задач, связанных с углами и тригонометрическими функциями.
Использование геометрического определения котангенса на единичной окружности помогает наглядно представить значение котангенса и увидеть связь между функцией и углом в треугольнике.
Геометрическое определение котангенса
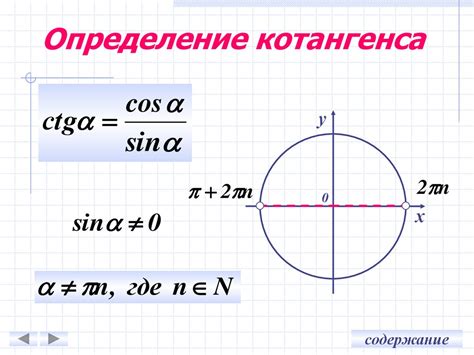
Геометрическое определение котангенса базируется на единичной окружности и позволяет найти значение котангенса для любого угла.
Для начала, нам нужно понять, какие значения соответствуют различным углам на единичной окружности. Для этого, мы будем рассматривать углы относительно начала координат.
Единичная окружность представляет собой окружность радиусом 1 и центром в начале координат (0, 0). Любая точка на этой окружности задается парой углов (θ, 1), где θ - угол от оси X до луча, и 1 - расстояние от начала координат до точки на окружности.
Котангенс угла θ определяется как отношение противоположной стороны (x) к прилежащей стороне (y) в прямоугольном треугольнике, верхний катет которого лежит на единичной окружности и радиусе, проведенном из начала координат до точки с углом θ.
| Угол θ | Kot(θ) |
|---|---|
| 0° (0) | бесконечность |
| 30° (π/6) | √3/3 |
| 45° (π/4) | 1 |
| 60° (π/3) | √3 |
| 90° (π/2) | 0 |
| 180° (π) | -бесконечность |
Другие значения котангенса могут быть найдены, используя симметрию и периодичность функции котангенса.
Геометрическое определение котангенса на единичной окружности играет важную роль в тригонометрии и многих ее применениях.
Единичная окружность

Преимущества использования единичной окружности:
- Простота вычислений: так как радиус окружности равен единице, все значения координат точек на окружности являются простыми числами.
- Удобство визуализации: благодаря своему радиусу и центру в начале координат, единичная окружность легко визуализируется и помогает понять геометрические свойства функций.
- Универсальность: единичная окружность встречается во множестве областей, включая геометрию, тригонометрию, физику и компьютерную графику.
Единичная окружность также играет важную роль в нахождении котангенса и других тригонометрических функций. Геометрические определения позволяют легко вычислять значения этих функций и использовать их в различных задачах.
Как найти котангенс на единичной окружности

Для нахождения котангенса угла на единичной окружности нужно провести перпендикуляр из точки окружности на ось абсцисс и отложить его длину вдоль оси абсцисс. Затем, проведя радиус в вершину угла, образованного перпендикуляром и радиусом окружности, можно найти прилежащий и противоположный катеты треугольника.
Прилежащий катет равен абсциссе точки пересечения перпендикуляра и оси абсцисс. Противоположный катет равен ординате этой точки. Поделив прилежащий катет на противоположный, получим котангенс угла.
Формула для нахождения котангенса на единичной окружности:
- Найдите абсциссу точки пересечения перпендикуляра и оси абсцисс.
- Найдите ординату этой точки.
- Поделите абсциссу на ординату, чтобы найти котангенс угла.
Таким образом, используя геометрическое определение котангенса на единичной окружности, можно легко вычислить значение данной функции для различных углов.