Котангенс угла – это одна из тригонометрических функций, которая находит свое применение в решении многих задач. Для нахождения значения котангенса угла $\alpha$ существует несколько способов, которые могут быть полезны при работе с треугольниками и геометрическими объектами. Знание этих способов позволит упростить расчеты и освоить базовые принципы тригонометрии.

Первый способ основан на использовании соотношений между тригонометрическими функциями исходного угла. Котангенс угла $\alpha$ можно выразить через тангенс: $\cot(\alpha) = \frac{1}{\tan(\alpha)}$. Таким образом, если известно значение тангенса угла $\alpha$, можно найти его котангенс по формуле.

Второй способ основан на использовании геометрического представления котангенса. Котангенс угла $\alpha$ определяется как отношение прилежащего катета к противолежащему катету в прямоугольном треугольнике, где гипотенуза является стороной противолежащей углу $\alpha$. Таким образом, если известны длина прилежащего и противолежащего катетов, можно найти котангенс угла $\alpha$ с использованием простых геометрических соотношений.

Использование этих способов позволяет быстро и удобно находить значение котангенса угла $\alpha$ в тригонометрии. При решении задач, связанных с треугольниками и геометрическими объектами, знание этих способов может оказаться очень полезным.

Что такое котангенс?

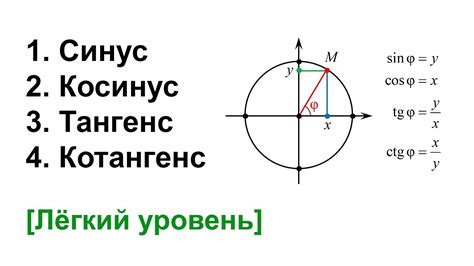
Котангенс угла а обозначается как cot a и определяется как отношение катета прилегающего к углу к катету противоположному:

cot a = adjacent/opposite

Таким образом, котангенс угла а показывает, сколько раз отношение длины прилегающего катета к длине противоположного катета помещается в единицу. Или, иначе говоря, это обратное значение тангенса угла а.

Котангенс угла может быть положительным или отрицательным, в зависимости от значения угла. Если угол находится в первой или третьей четверти, то котангенс положителен, а если во второй или четвертой, то отрицателен.

Наличие котангенса в тригонометрии позволяет более полно описывать геометрические и физические явления, связанные с углами и отношениями сторон треугольника. Например, котангенс может использоваться для нахождения высоты треугольника, расстояния до точки отрезка или градиента, а также для решения более сложных задач, связанных с тригонометрическими функциями.

Интересный факт о котангенсе

Математически это можно записать следующим образом:

ctg(a) = cos(a) / sin(a)

Таким образом, котангенс угла a представляет собой отношение катета, лежащего рядом с углом a, к катету, противолежащему углу a, в прямоугольном треугольнике с гипотенузой равной 1. Это полезное свойство котангенса позволяет нам вычислять его не только как обратную функцию тангенса, но и через отношение косинуса и синуса угла.

Использование этого свойства позволяет упростить вычисления и приводит к более эффективным способам нахождения котангенса угла в тригонометрии.

Интересно то, как разные математические свойства и определения могут удивить нас и помочь нам лучше понять и использовать тригонометрию в нашей повседневной жизни.

Связь котангенса с синусом и косинусом

Котангенс угла a в тригонометрии можно определить, используя соотношение между синусом и косинусом этого угла. Котангенс a обратно пропорционален синусу a и косинусу a. Другими словами, котангенс a равен отношению косинуса a к синусу a.

Математически это можно записать следующим образом:

cot a = cos a / sin a

Таким образом, чтобы найти котангенс угла a, необходимо вычислить значение косинуса и синуса этого угла и затем разделить значение косинуса на значение синуса.

Например, если известно, что косинус угла a равен 0.6, а синус угла a равен 0.8, то котангенс угла a можно найти следующим образом:

cot a = 0.6 / 0.8 = 0.75

Итак, связь котангенса с синусом и косинусом угла a позволяет находить значение котангенса, если известны значения синуса и косинуса этого угла.

Первый способ нахождения котангенса угла а

Для нахождения котангенса угла a по его синусу (sin a) и косинусу (cos a), воспользуемся следующей формулой:

ctg a = cos a / sin a

Чтобы упростить вычисления, можно воспользоваться определением тригонометрических функций на единичной окружности. В данном случае, косинус угла a будет равен x-координате точки на единичной окружности, соответствующей углу a, а синус угла a - y-координате.

Итак, сначала нужно найти косинус и синус угла a с помощью таблиц или калькулятора. Затем подставить эти значения в формулу и произвести вычисления, чтобы получить значение котангенса угла a.

Второй способ нахождения котангенса угла а

Если известны значения синуса и косинуса угла а, то котангенс этого угла можно найти следующим образом:

1. Воспользуемся определением котангенса: cot(а) = 1 / tan(а).

2. Используем соотношение между тангенсом, синусом и косинусом: tan(а) = sin(а) / cos(а).

3. Подставим найденное значение тангенса в формулу для котангенса: cot(а) = 1 / (sin(а) / cos(а)).

4. Сократим выражение, поменяв деление на умножение и получим окончательную формулу: cot(а) = cos(а) / sin(а).

Таким образом, если даны значения синуса и косинуса угла а, можно легко найти значение котангенса угла, применив указанный способ.