Критические точки функции являются одним из ключевых понятий математического анализа и играют важную роль в определении поведения функций. Калькулятор позволяет найти эти точки с помощью нескольких методов, которые помогут вам в этом процессе.
Первый метод – использование производной функции. Производная функции показывает, как меняется значение функции при изменении аргумента. Если производная функции равна нулю в какой-то точке, то эта точка является критической. После нахождения всех таких точек, нужно проанализировать значение производной в соседних точках, чтобы определить, является ли точка экстремумом или седловой точкой.
Еще один метод заключается в решении уравнения на производную функцию. Если найти такие значения аргумента, при которых производная функции равна нулю или не определена, то получены критические точки. Чтобы понять их природу, нужно анализировать вторую производную функции.
Роль критических точек
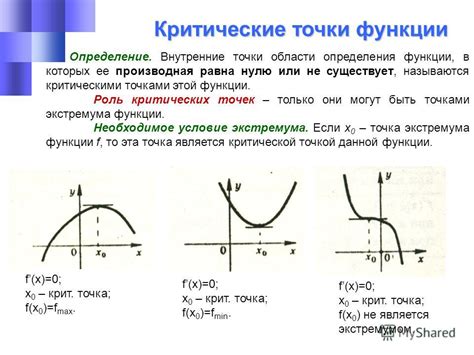
Анализ критических точек позволяет определить экстремумы функции, то есть места, где функция достигает своих наибольших или наименьших значений. Кроме того, критические точки могут указывать на изменение выпуклости функции и наличие перегибов.
Для нахождения критических точек необходимо найти производную функции и приравнять её к нулю. Затем решить полученное уравнение, чтобы найти значения аргументов, соответствующие критическим точкам. Далее следует применить исследование знаков производной, чтобы определить, является ли каждая критическая точка точкой минимума, максимума или перегиба.
Критические точки функции
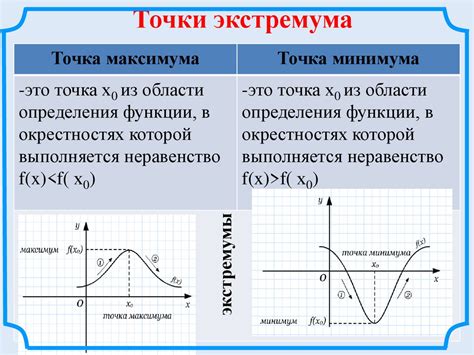
Решение задачи о нахождении критических точек функции позволяет определить экстремумы функции, то есть ее минимальные и максимальные значения. Критические точки также могут указывать на точки разрыва или особенности функции.
Чтобы найти критические точки функции, необходимо найти производную функции, приравнять ее к нулю и решить полученное уравнение. Если производная не существует в некоторой точке, это также является критической точкой.
Критические точки помогают определить поведение функции вблизи этих точек. Например, если функция имеет локальный минимум в критической точке, то в окрестности этой точки функция имеет тенденцию убывать.
Исследование критических точек функции играет важную роль в оптимизации и определении параметров функций. Для нахождения экстремумов функций, а также для определения областей монотонности и выпуклости графиков функций, необходимо провести анализ критических точек.
Важно отметить, что нахождение критических точек является лишь первым шагом в анализе функции. Для полного исследования поведения функции необходимо также определить точки разрыва и особенности, а также провести анализ графика функции на различных интервалах.
Определение критических точек
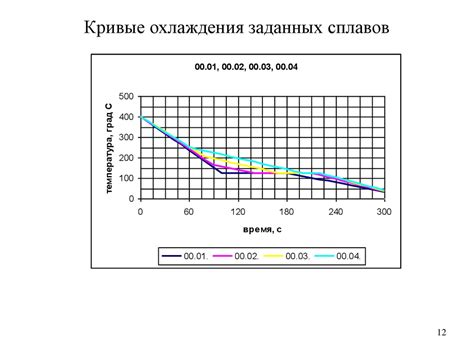
Определение критических точек является важным шагом при поиске экстремумов функции. Критические точки помогают нам определить, где функция достигает своего максимума или минимума.
Если производная функции равна нулю в точке, то это может указывать на наличие экстремума. Однако, следует также учесть, что наличие критической точки не всегда гарантирует наличие экстремума.
Если производная функции не существует в точке, то это может быть признаком разрыва функции или изменения ее поведения.
Поэтому, для определения критических точек функции необходимо проанализировать производную функции и найти ее корни и точки, в которых производная не существует.
Поиск критических точек
Существует несколько методов для поиска критических точек:
| Метод | Описание |
|---|---|
| Метод аналитического дифференцирования | Позволяет найти производную функции и найти точки, в которых она равна нулю или не существует. |
| Метод численного дифференцирования | Использует численные методы для приближенного вычисления производной функции и нахождения критических точек. |
| Графический метод | Позволяет найти критические точки, исследуя график функции и выявляя его перегибы и экстремумы. |
После нахождения критических точек, можно использовать теоремы анализа функций для определения их типа - максимумы, минимумы или точки перегиба.
Поиск критических точек важен для решения задач оптимизации и моделирования различных процессов. Он позволяет находить экстремумы функций и оптимальные значения параметров.
Методы нахождения критических точек
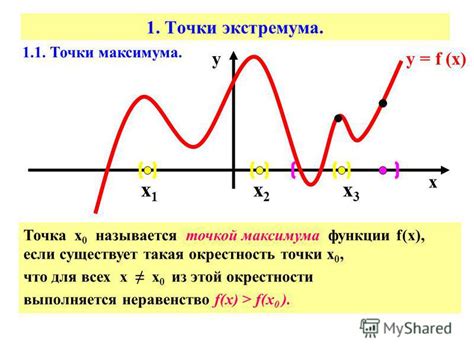
1. Метод дифференцирования. Для нахождения критических точек функции можно использовать процесс дифференцирования. Если производная функции равна нулю или не существует в какой-либо точке, то эта точка будет являться критической.
2. Метод экстремумов. Критические точки функции могут также быть найдены путем анализа экстремумов. Необходимо проверить, возможно ли достижение максимума или минимума функции в данной точке.
3. Метод подстановки. Для некоторых функций можно использовать метод подстановки значений, чтобы найти точки, в которых производная равна нулю или не существует.
4. Метод графического анализа. Построение графика функции может помочь визуально найти критические точки, где значение производной будет равным нулю или не существует.
5. Метод численного анализа. С использованием различных численных методов, таких как метод Ньютона или метод секущих, можно приближенно найти критические точки функции.
Каждый из этих методов имеет свои преимущества и может быть использован в зависимости от сложности функции и доступной информации о ней. Комбинирование различных методов может помочь получить более точные и полные результаты.
Производная и ее роль
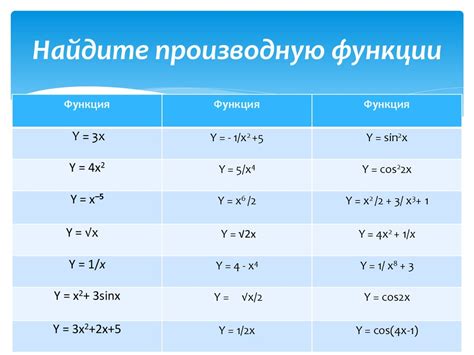
Для поиска критических точек функции применяется метод дифференцирования. Дифференцирование – это процесс нахождения производной функции. С помощью производной мы можем определить максимумы и минимумы функции, а также точки перегиба.
Рассмотрим пример: функция f(x) = x^2. Найдем производную этой функции: f'(x) = 2x. Из производной видно, что функция имеет нулевую производную в точке x = 0. Это означает, что функция имеет горизонтальную касательную в этой точке и может иметь экстремумы.
Производная является основным инструментом в оптимизации функций. Нахождение критических точек позволяет найти точки максимума или минимума функции, что является важным в различных областях, включая математику, физику, экономику и многие другие.