Квадратный корень числа - это значение, которое при возведении в квадрат даёт исходное число. На первый взгляд, поиск квадратного корня может показаться простой задачей, однако, при работе с большими числами или при необходимости провести множество вычислений, становится очевидным, что нужен эффективный подход.
Существует несколько методов нахождения квадратных корней, каждый из которых может быть эффективным в разных ситуациях. Один из самых простых методов - это метод перебора. Он заключается в последовательном переборе всех чисел от 0 до исходного числа, и проверке, является ли возведение в квадрат текущего числа равным исходному числу. Однако, данный метод работает медленно и не подходит для поиска квадратного корня больших чисел.
Более эффективными методами являются методы Ньютона и Бабилона. Метод Ньютона основан на итеративном приближении квадратного корня через производную функции, которая содержит искомое значение. Он является итерационным методом и обеспечивает сходимость к корню с заданной точностью. Метод Бабилона работает на основе итераций, но выражается через последовательность средних арифметических между исходным числом и текущим приближением к корню.
Выбор оптимального метода для нахождения квадратного корня будет зависеть от конкретной задачи и требуемой точности. Несмотря на то, что существуют эффективные алгоритмы, поиск квадратного корня остается важной и интересной задачей в области математики и программирования.
Квадратный корень числа: методы и алгоритмы

Существует несколько методов и алгоритмов нахождения квадратного корня числа. Один из наиболее распространенных методов - метод Ньютона, также известный как метод касательных. Он основан на итерационном процессе, который позволяет приближенно находить квадратный корень числа. Этот метод особенно полезен при нахождении квадратного корня больших чисел.
Другой распространенный метод - метод деления пополам, который основан на принципе бинарного поиска. Он заключается в том, чтобы сравнивать серединное значение с исходным числом и продолжать делить интервал пополам, пока не будет достигнута необходимая точность. Этот метод часто используется для нахождения квадратного корня целых чисел.
Также существуют другие алгоритмы и методы нахождения квадратного корня числа, такие как метод Герона, метод Бабили, метод Штурма и другие. Каждый из них имеет свои преимущества и недостатки, и выбор конкретного метода зависит от требуемой точности, скорости вычислений и других факторов.
Важно отметить, что нахождение квадратного корня числа является необходимым шагом для решения других математических задач, таких как нахождение обратного числа, вычисление синуса, косинуса и других функций. Поэтому эффективное нахождение квадратного корня числа имеет большое значение в различных областях науки и техники.
Поиск квадратного корня числа через итерационные методы

Один из способов решения этой задачи - использование итерационных методов. Итерационные методы основываются на итеративном приближении значения квадратного корня с заданной точностью.
Один из наиболее популярных итерационных методов - метод Ньютона. Этот метод основан на использовании последовательных приближений:
Шаг 1: Задаем начальное приближение y0.
Шаг 2: Вычисляем следующее приближение yn+1 по формуле: yn+1 = 0.5 * (yn + (x/yn)).
Шаг 3: Повторяем Шаг 2 до достижения требуемой точности.
Этот метод позволяет находить квадратный корень с высокой точностью и эффективно, особенно при работе с большими числами. Однако, он также требует начального приближения, которое может влиять на скорость сходимости.
Итерационные методы находят применение во многих областях, включая финансовый анализ, машинное обучение и компьютерную графику. Нахождение квадратного корня числа - это только один пример использования этих методов и позволяет лучше понять их принцип работы и преимущества.
Бинарный поиск квадратного корня числа
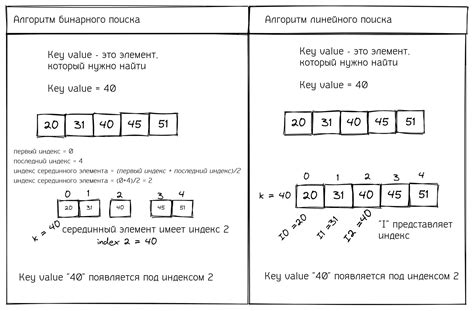
Алгоритм бинарного поиска квадратного корня следующий:
- Выбирается начальный диапазон, в котором находится искомое значение. Например, для положительного числа x начальный диапазон будет [0, x].
- Пока диапазон не станет достаточно маленьким (например, меньше заданной точности), выполняются следующие шаги:
- Находится среднее значение диапазона (медиана).
- Сравнивается значение медианы с квадратом искомого числа:
- Если значение медианы меньше квадрата искомого числа, то искомое значение находится в правой половине диапазона.
- Если значение медианы больше квадрата искомого числа, то искомое значение находится в левой половине диапазона.
- Если значение медианы равно квадрату искомого числа, то это является точным значением квадратного корня.
Бинарный поиск квадратного корня является эффективным методом, особенно для больших чисел, так как позволяет сократить количество итераций по сравнению с методами перебора или применения математических функций. Однако стоит учитывать, что он может быть несколько сложнее для реализации по сравнению с другими методами.
Метод Ньютона для нахождения квадратного корня числа

Основная идея метода заключается в следующем: начиная с некоторого приближения, мы строим касательную к графику функции и находим точку пересечения этой касательной с осью абсцисс. Затем мы повторяем этот процесс, используя новую точку пересечения в качестве приближенного значения, пока не достигнем достаточно точного ответа.
Математически он может быть формализован следующим образом:
Шаг 1: Задаем начальное приближение x0.
Шаг 2: Вычисляем новое приближение x1 по формуле:
x1 = (x0 + (n / x0)) / 2,
где n - исходное число, для которого мы ищем квадратный корень.
Шаг 3: Повторяем Шаг 2, пока разница между x1 и x0 не будет меньше заданной точности.
Применение метода Ньютона для нахождения квадратного корня числа позволяет достичь высокой скорости сходимости. Однако, его эффективность может снизиться, если начальное приближение выбрано неправильно или если функция имеет локальные экстремумы в окрестности корня.
Приближенное вычисление квадратного корня числа методом Герона

Основная идея метода Герона заключается в следующем:
- Выбирается начальное приближение квадратного корня, например, a/2.
- Выполняется итерационный процесс, в котором текущее приближение квадратного корня уточняется по формуле:
- Шаги 2 и 3 повторяются до тех пор, пока разница между текущим приближением и предыдущим приближением не станет достаточно малой.
xn+1 = (xn + a / xn) / 2
Метод Герона обеспечивает быструю итерацию и сходится к истинному значению квадратного корня достаточно быстро. Он хорошо подходит для компьютерных вычислений и обладает большой точностью.
Данный метод широко используется в различных областях вычислительной математики, таких как анализ данных, обработка сигналов и машинное обучение. Он может быть реализован на различных программных и аппаратных платформах, что делает его универсальным и доступным инструментом для решения различных задач приближенного вычисления квадратного корня числа.
Важно отметить, что метод Герона имеет свои ограничения и некоторые особенности. Например, он может не сходиться для отрицательных чисел или чисел близких к нулю. Также он может быть чувствителен к некоторым видам ошибок округления. Поэтому при использовании метода Герона необходимо учитывать данные ограничения и особенности для получения точных результатов.
Рациональное и иррациональное число в контексте квадратного корня
Результатом вычисления квадратного корня является число, которое при возведении в квадрат равно исходному числу. Известно, что квадратный корень из отрицательного числа не является рациональным числом, поскольку не существует рационального числа, возведение в квадрат которого даёт отрицательный результат.
Следовательно, квадратный корень из отрицательного числа является комплексным числом, которое имеет мнимую и вещественную часть. Комплексные числа представлены в виде a + bi, где a - вещественная часть, а bi - мнимая часть.
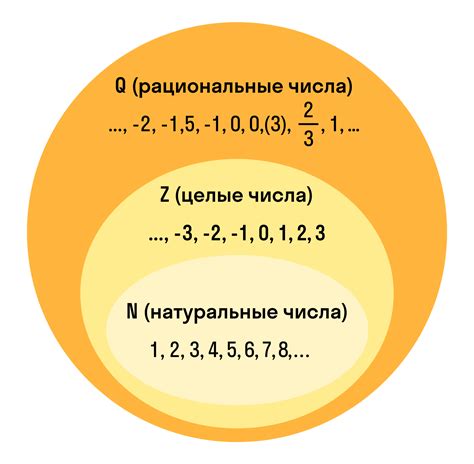
С другой стороны, квадратный корень из положительного числа может быть как рациональным, так и иррациональным числом. Рациональные числа представляются в виде обыкновенных дробей, например, 2/3 или -5/7. Рациональные числа могут быть выражены конечной или периодической десятичной дробью.
Иррациональные числа не могут быть представлены в виде обыкновенных дробей и имеют бесконечную десятичную запись, которая не повторяется или не обладает периодичностью. Примеры иррациональных чисел в контексте квадратного корня включают √2, π и е. Иррациональные числа являются важными в математике и участвуют в различных математических доказательствах и теориях.
Важно отметить, что квадратный корень из некоторых рациональных чисел также может быть иррациональным числом. Например, квадратный корень из 2 является иррациональным числом, хотя 2 само является рациональным числом. Это отношение между рациональными и иррациональными числами делает квадратный корень интересным объектом изучения в математике.
| Тип числа | Примеры |
|---|---|
| Рациональное число | 2, -5/7, 0.75 |
| Иррациональное число | √2, π, е |
| Комплексное число | 3 + 4i, -2 - 6i |
Изучение рациональных и иррациональных чисел в контексте квадратного корня позволяет нам лучше понять свойства чисел и развивать эффективные методы для нахождения квадратного корня числа.
Связь между квадратным корнем и возведением в степень

Возведение в степень и вычисление квадратного корня являются обратными операциями. Если мы возведем число в степень 2, то получим его квадрат, а если извлечем квадратный корень из числа, то получим число, возводя которое в квадрат, получим исходное число.
Существует несколько методов и алгоритмов для эффективного вычисления квадратного корня, включая методы Ньютона и бинарного поиска. Эти методы основаны на итеративных вычислениях и последовательных приближениях.
Знание связи между квадратным корнем и возведением в степень поможет нам лучше понять и применять эти методы для нахождения квадратного корня числа эффективно.
Применение квадратного корня в различных областях науки и техники

В физике, квадратный корень используется для определения длины стороны прямоугольного треугольника по формуле Пифагора. Это позволяет вычислять расстояния, скорости и ускорения в двумерном и трехмерном пространстве.
В инженерии, квадратный корень используется для определения длины сторон форм равенства и полноты до элементов конструкции. Например, в строительстве он позволяет определить длину кабеля, требуемую для соединения двух точек.
В финансовой математике, квадратный корень используется для определения среднеквадратического отклонения и волатильности ценных бумаг и инвестиционных портфелей. Это позволяет инвесторам оценивать риск и прогнозировать доходность своих инвестиций.
В компьютерной графике, квадратный корень используется для определения расстояния между двумя точками в трехмерном пространстве. Это позволяет создавать реалистичные эффекты освещения и тени на графических моделях и сценах.
В машинном обучении, квадратный корень используется для вычисления ошибки модели и определения ее точности. Это позволяет улучшать алгоритмы обучения и создавать более эффективные модели предсказания.
В общем, квадратный корень имеет широкий спектр применений в науке и технике. Он позволяет решать различные задачи, требующие точных вычислений и оценок. Понимание методов и алгоритмов нахождения квадратного корня может быть полезным инструментом для ученых, инженеров и аналитиков в различных областях.